# A tibble: 1 × 1
mean
<dbl>
1 174.Summarizing data, a Review
Lucy D’Agostino McGowan
Learning objectives
- Recall how to summarize one continuous variable
- Identify variables where a mean is a good summary measure (or not)
- Explain why we summarize data (what is the big picture?)
Application Exercise
bit.ly/sta-112-f22-appex-05
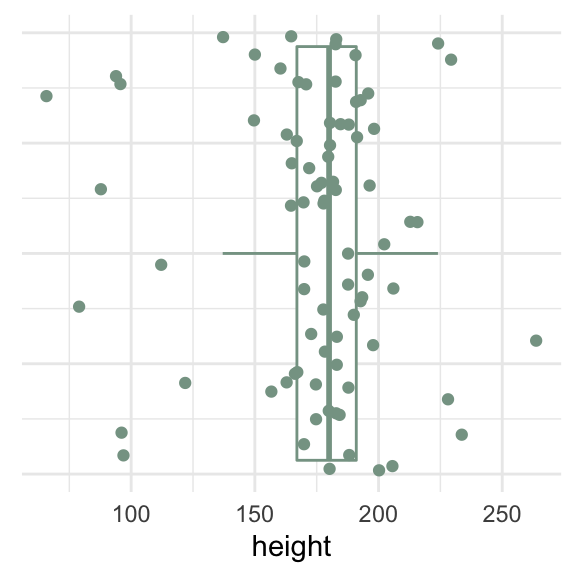
One continuous variable
One continuous variable
How can we visualize a single continuous variable?
Histogram
Code
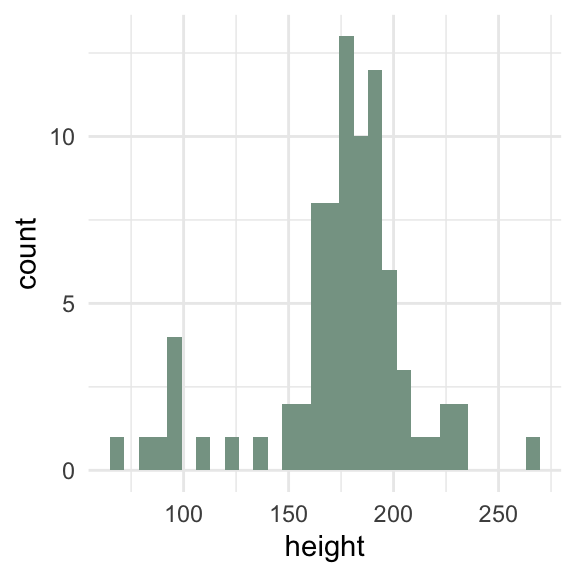
Density
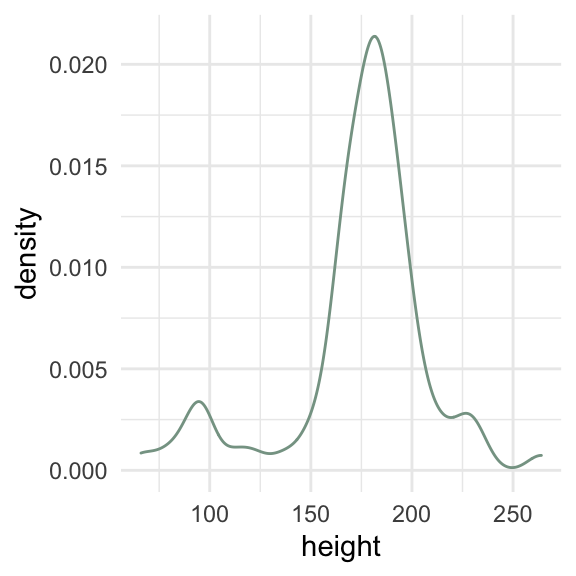
One continuous variable
How can we numerically summarize a single continuous variable?
One continuous variable
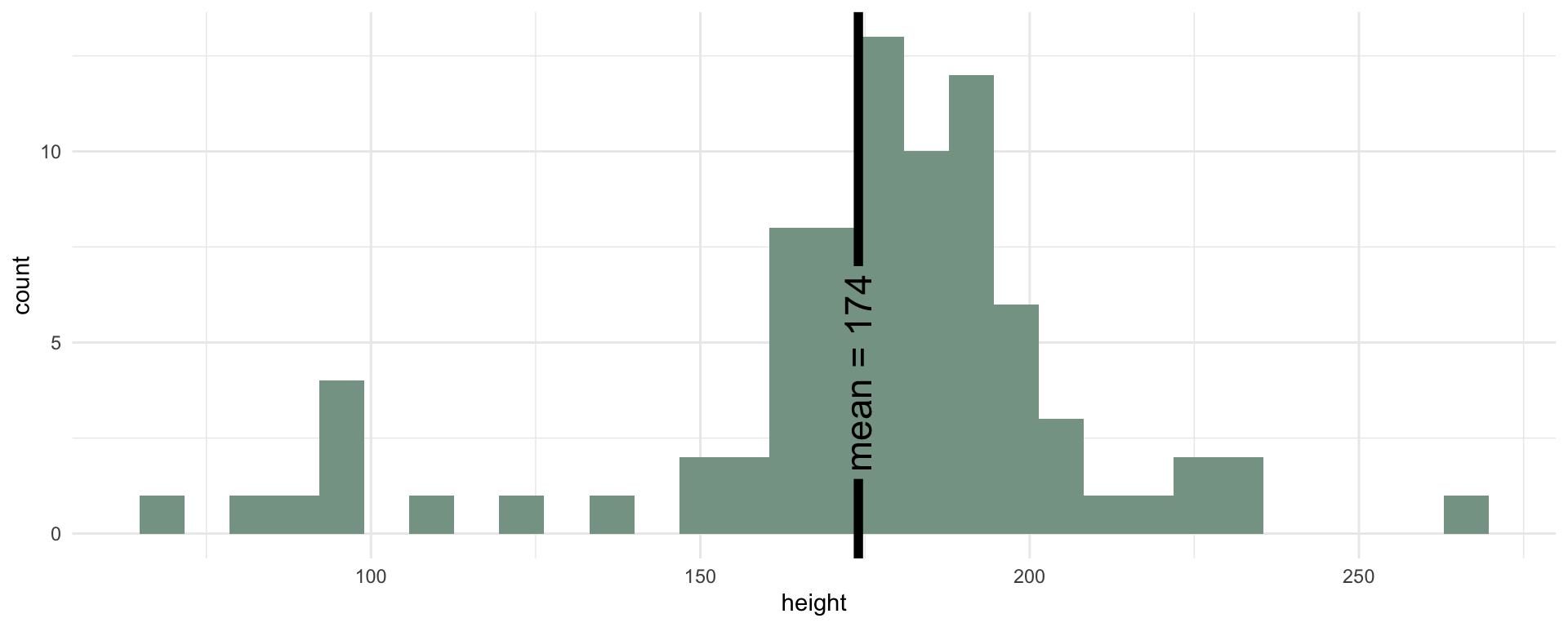
One continuous variable
Why do we calculate a mean?
- Reduces the dimensionality of the data (from
nto1) - To get a sense of a “typical” observation
- When is this an accurate representation?
Meaningful means
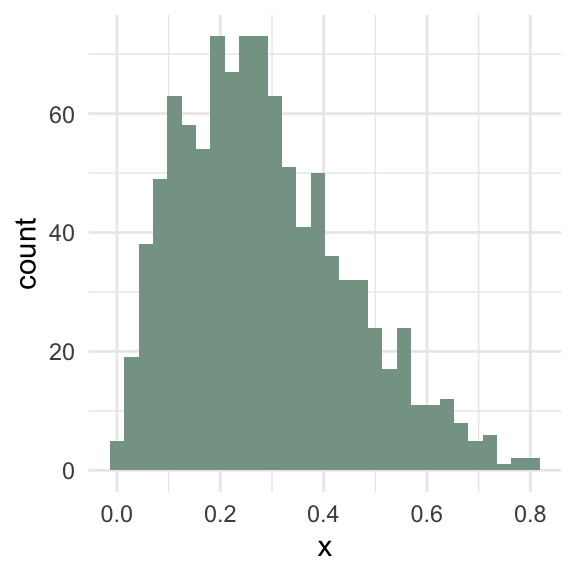
Symmetric
Code
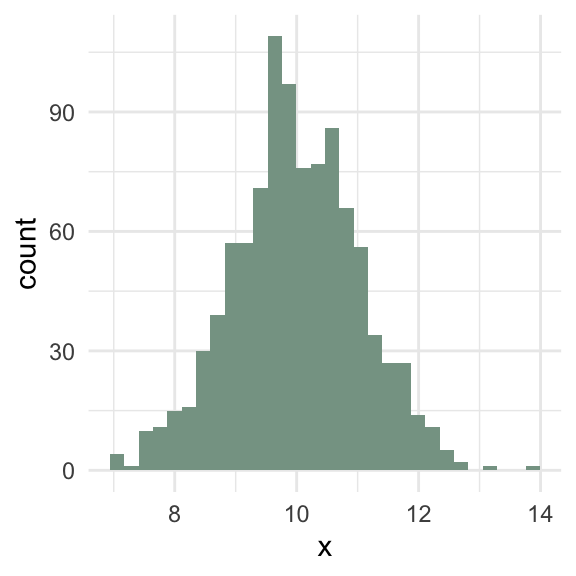
Bimodal
Code
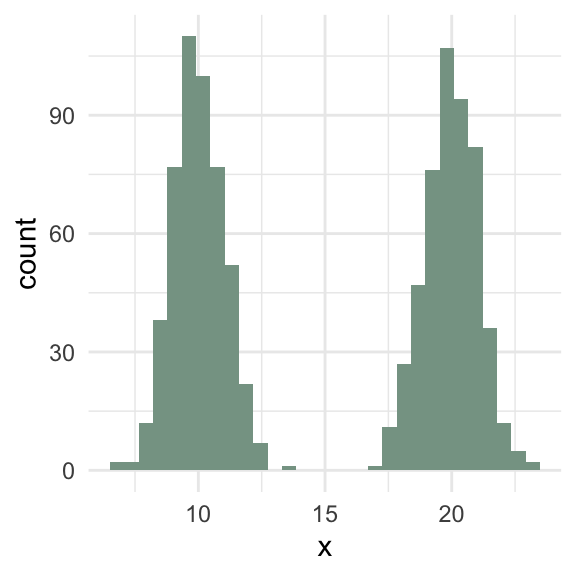
Guess the mean for each of these variables.
Meaningful means
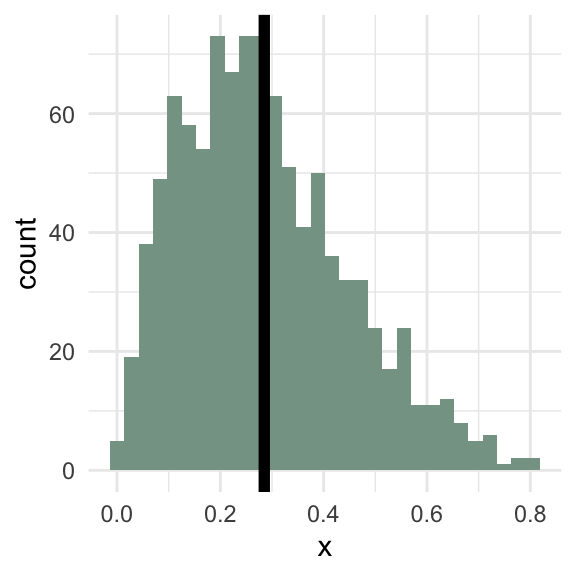
Symmetric
Code
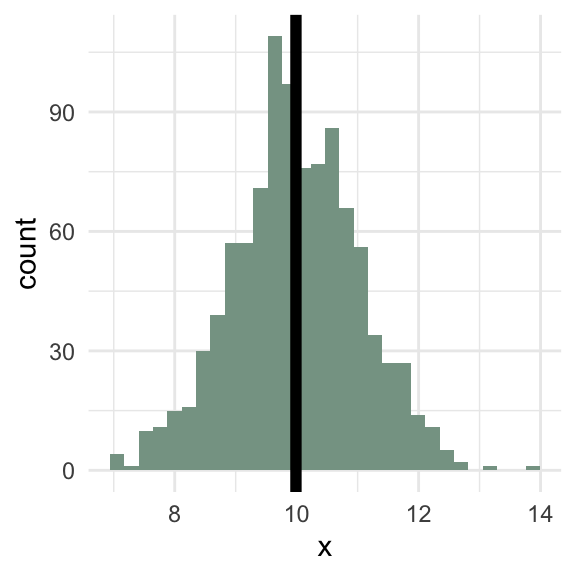
Bimodal
Code
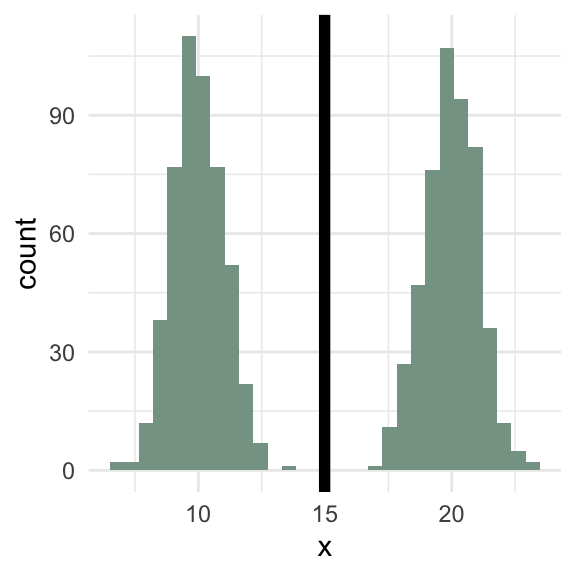
Does this value represent a “typical” observation?
Math speak
\[\Large\bar{x} =\sum_{i=1}^n \frac{x_i}{n}\]
Math speak
\[\Large{\require{color}\colorbox{#86a293}{$\bar{x}$}} =\sum_{i=1}^n \frac{x_i}{n}\]
the mean of the variable \(x\)
Math speak
\[\Large\bar{x} ={\require{color}\colorbox{#86a293}{$\sum$}}_{i=1}^n \frac{x_i}{n}\]
add up the observations
Math speak
\[\Large\bar{x} =\sum_{{\require{color}\colorbox{#86a293}{$i=1$}}}^n \frac{x_i}{n}\]
from the first
Math speak
\[\Large\bar{x} =\sum_{i=1}^{\require{color}\colorbox{#86a293}{$n$}} \frac{x_i}{{\require{color}\colorbox{#86a293}{$n$}}}\]
total number of observations
Math speak
\[\Large\bar{x} =\sum_{i=1}^n \frac{{\require{color}\colorbox{#86a293}{$x_i$}}}{n}\]
continuous variable for observation i
Math speak
\[\Large\bar{x} =\sum_{i=1}^n \frac{x_i}{\require{color}\colorbox{#86a293}{${n}$}}\]
divide by the total number of observations
Application Exercise
| data | |
|---|---|
| \(x_1\) | 3 |
| \(x_2\) | 5 |
| \(x_3\) | 1 |
| \(x_4\) | 7 |
| \(x_5\) | 8 |
- Using the data to the left, what is \(n\)?
- What is \(\bar{x}\)?
03:00
Data = model + error
Data
Data
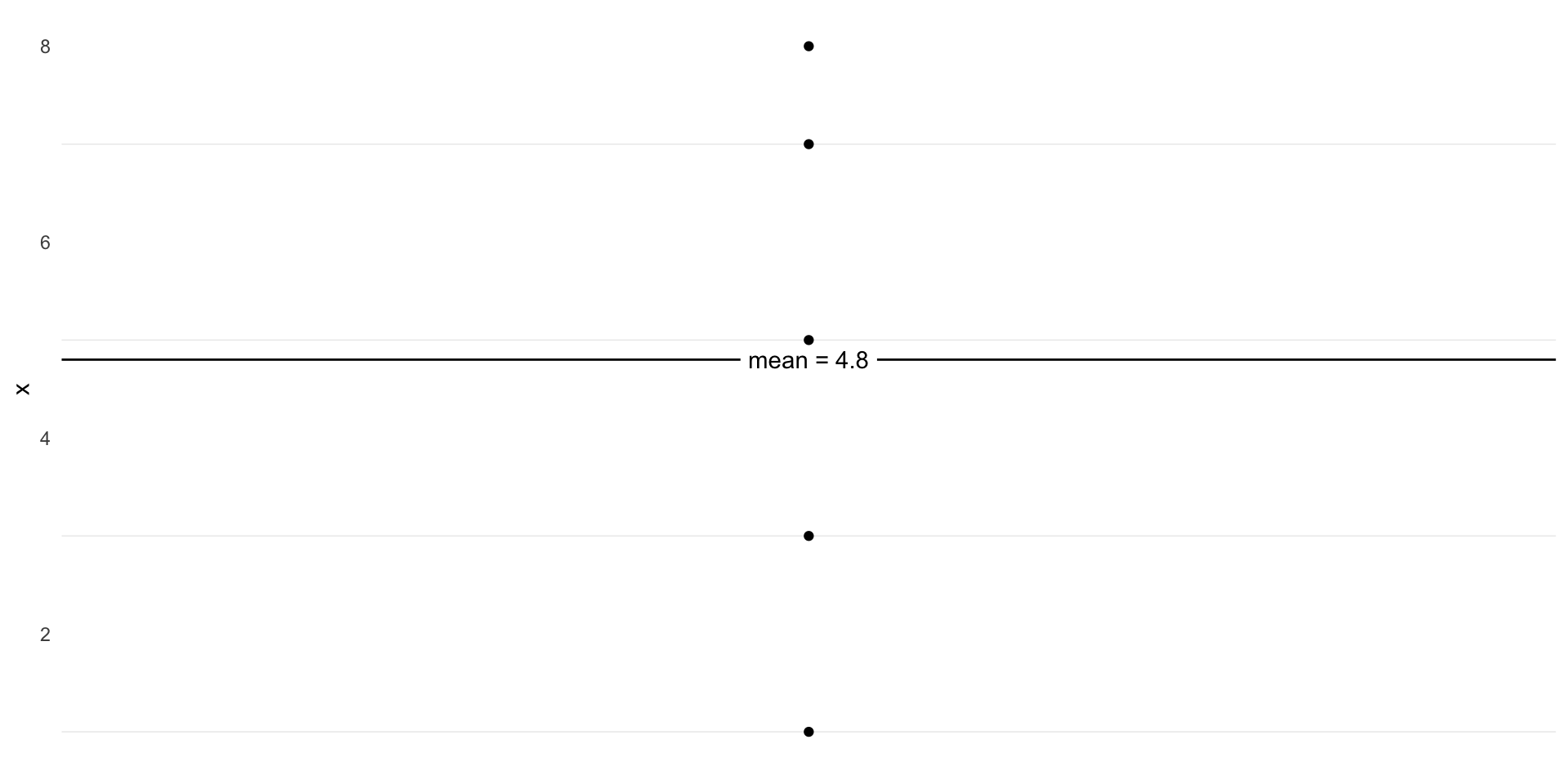
Data
Code
ggplot(d, aes(x = i, y = x)) +
geom_point() +
geom_texthline(yintercept = mean(d$x), label = "mean = 4.8") +
geom_segment(aes(y = x, yend = mean(x), x = i, xend = i), color = "blue") +
theme(axis.ticks.x = element_blank(),
axis.title.x = element_blank(),
axis.text.x = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor.x = element_blank())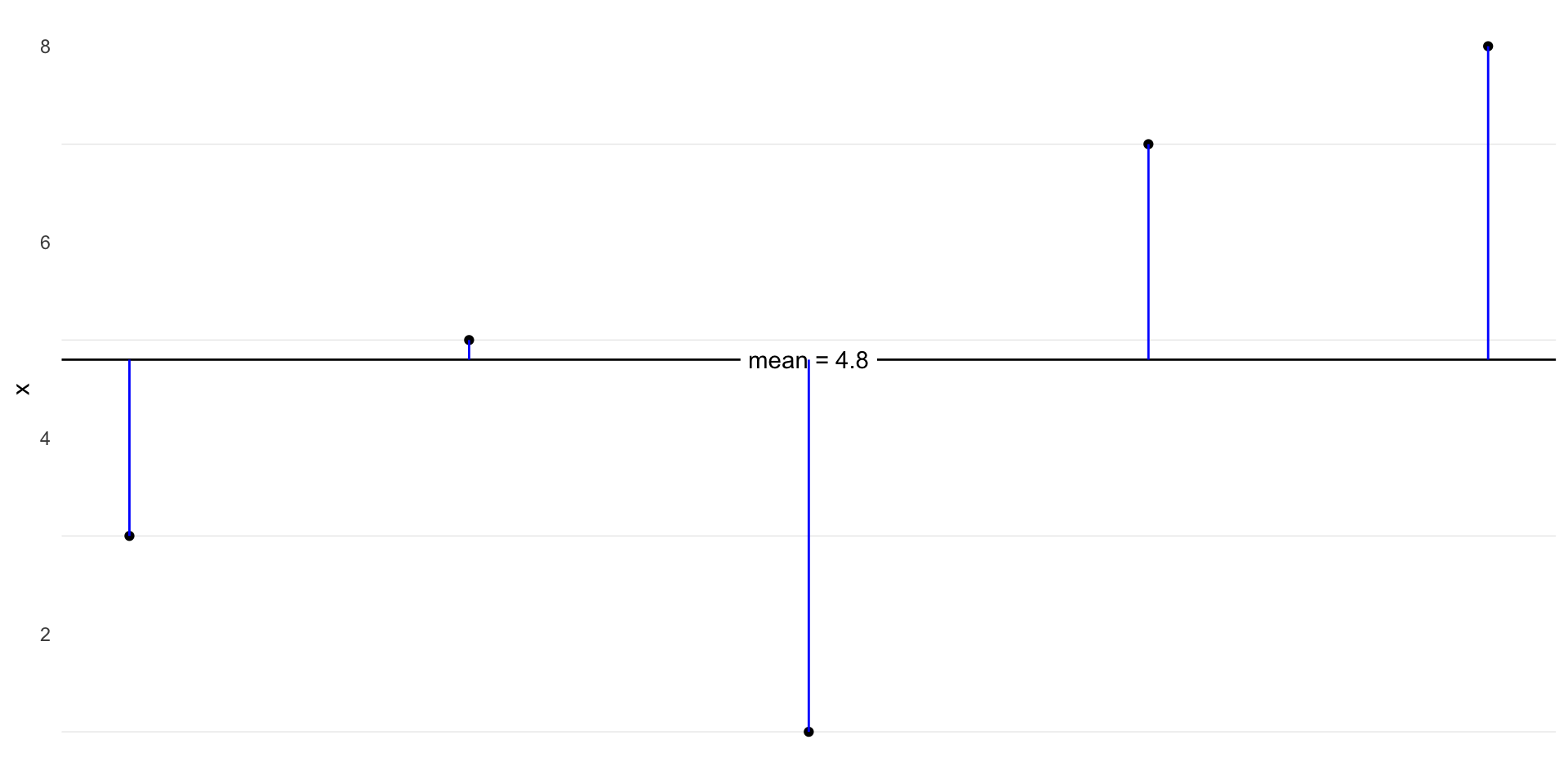
Math Speak
\[\Large x = \beta_0 + \varepsilon\]
Math Speak
\[\Large {\require{color}\colorbox{#86a293}{$x$}} = \beta_0 + \varepsilon\]
This is the vector \(x=\{x_1,\dots,x_n\}\)
Math Speak
\[\Large x = {\require{color}\colorbox{#86a293}{$\beta_0$}} + \varepsilon\]
we call this the “intercept”, when there are no other variables, it is just the mean, \(\bar{x}\)
Math Speak
\[\Large x = \beta_0 + {\require{color}\colorbox{#86a293}{$\varepsilon$}}\]
the error
Data
Code
ggplot(d, aes(x = i, y = x)) +
geom_point() +
geom_texthline(yintercept = mean(d$x), lwd = 5, hjust = 0.1,
label = as.character(expression(beta[0])), parse = TRUE) +
geom_segment(aes(y = x, yend = mean(x), x = i, xend = i), color = "blue") +
theme(axis.ticks.x = element_blank(),
axis.title.x = element_blank(),
axis.text.x = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor.x = element_blank()) 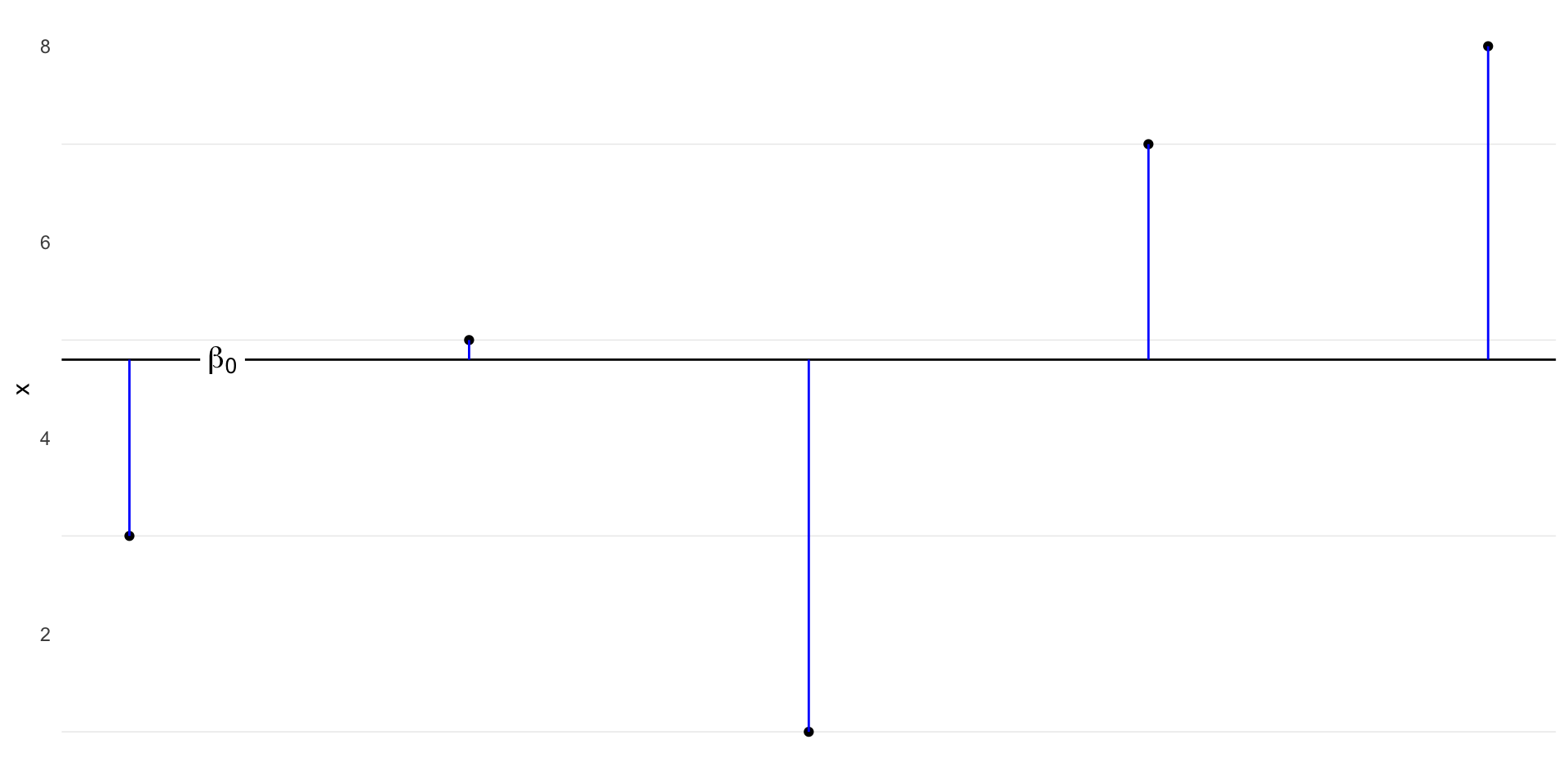
Data
Code
ggplot(d, aes(x = i, y = x)) +
geom_point() +
geom_texthline(yintercept = mean(d$x), lwd = 5, hjust = 0.1,
label = as.character(expression(beta[0])), parse = TRUE) +
geom_textsegment(aes(y = x, yend = mean(x), x = i, xend = i), color = "blue",
label = as.character(expression(epsilon)), parse = TRUE,
lwd = 5) +
theme(axis.ticks.x = element_blank(),
axis.title.x = element_blank(),
axis.text.x = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor.x = element_blank())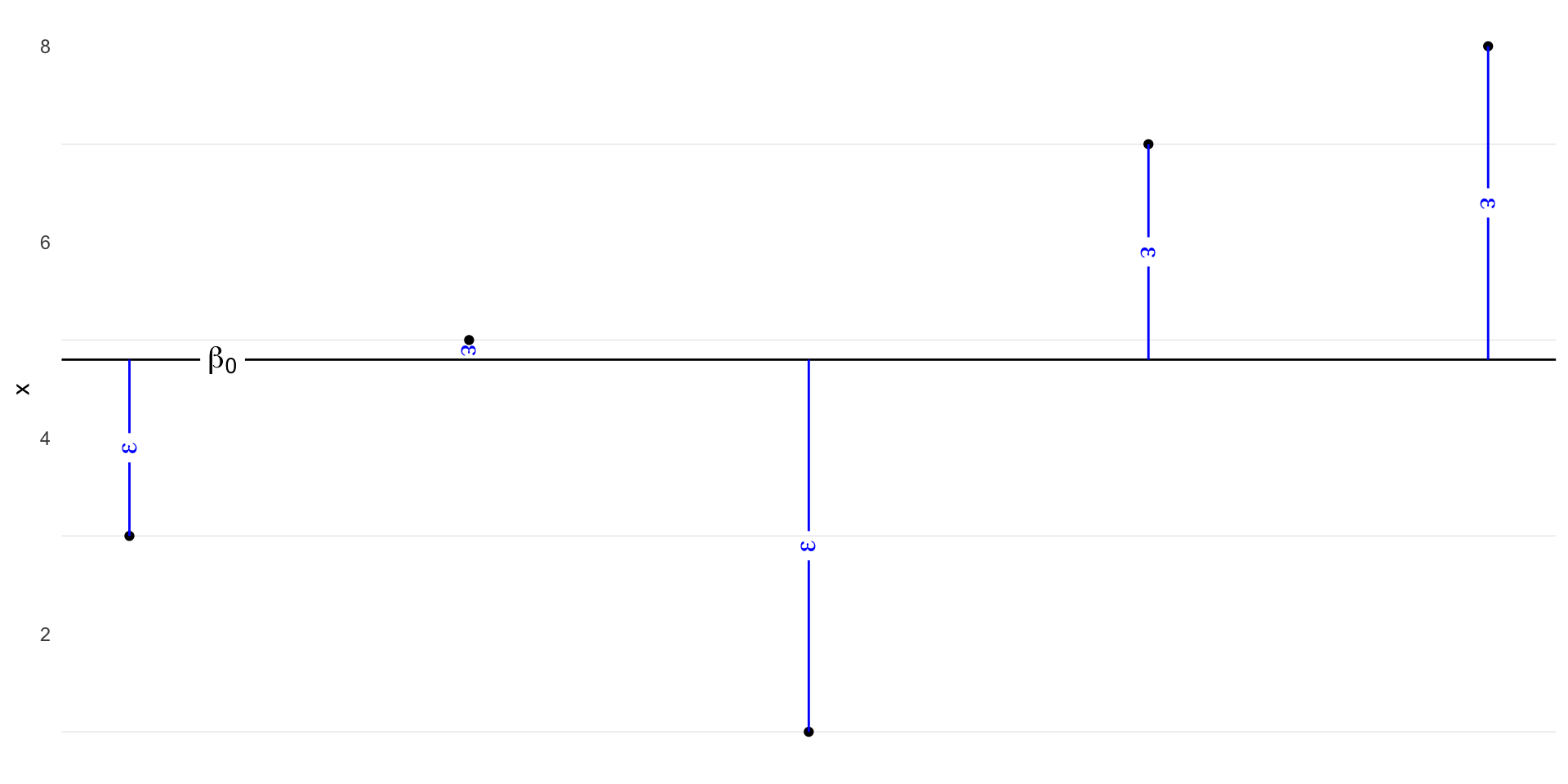
Data
Code
ggplot(d, aes(x = 1, y = x)) +
geom_point() +
geom_texthline(yintercept = mean(d$x), lwd = 5, hjust = 0.1,
label = as.character(expression(beta[0])), parse = TRUE) +
geom_segment(aes(y = x, yend = mean(x), x = 1, xend = 1), color = "blue") +
theme(axis.ticks.x = element_blank(),
axis.title.x = element_blank(),
axis.text.x = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor.x = element_blank()) 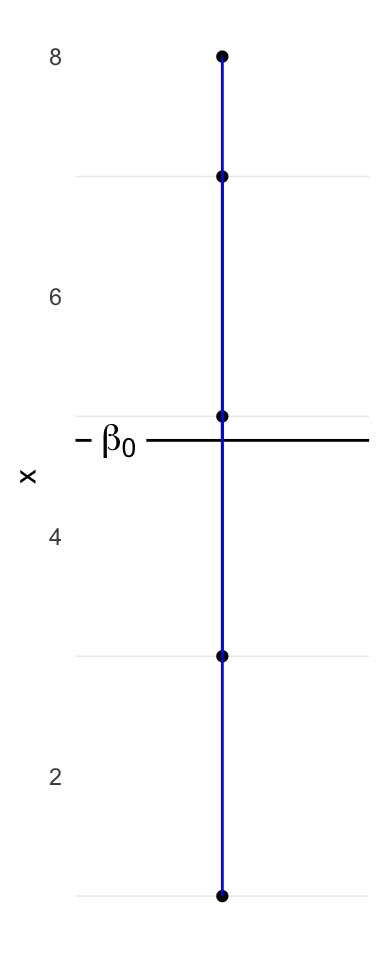
Data
Code
ggplot(d, aes(x = 1, y = x)) +
geom_point() +
geom_texthline(yintercept = mean(d$x), lwd = 5, hjust = 0.1,
label = as.character(expression(beta[0])), parse = TRUE) +
geom_segment(aes(y = x, yend = mean(x), x = 1, xend = 1), color = "blue") +
theme(axis.ticks.x = element_blank(),
axis.title.x = element_blank(),
axis.text.x = element_blank()) 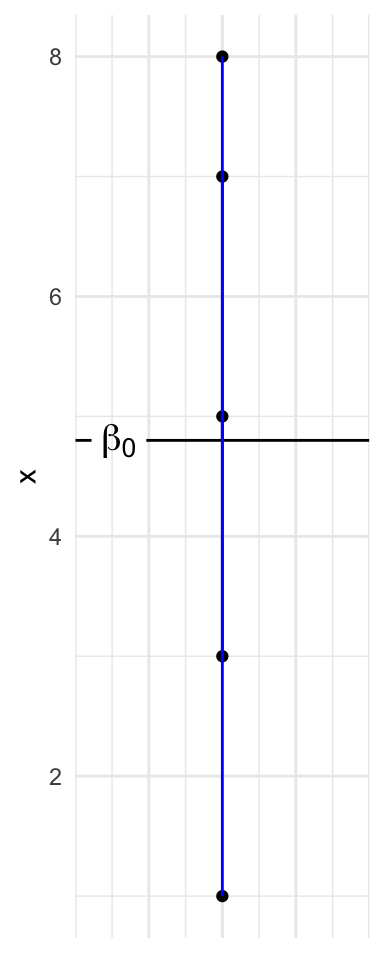
Calculating the mean in R
- “intercept only model”
lm: linear model
Application Exercise
Open your 04-appex.qmd file. Load the packages by running the top R chunk of code.
- Copy the code below into an R chunk at the bottom of the file:
What do you think this code does? Try typing ?tibble in the Console - what does this function do?
- Calculate the
meanofx. Do this two ways, using thesummaryfunction and using thelmfunction. - Add a new variable called
errorto the data setdthat is equal toxminus the mean of x.
05:00
Recap
When is the mean an appropriate summary measure to calculate?
What assumptions need to be true in order to use a mean to represent your single continuous variable?
![]()