Code
Lucy D’Agostino McGowan
What goes wrong if the relationship between \(x\) and \(y\) isn’t linear?

\(\hat\beta_1\) = 2 (95% CI: 1.79, 2.21)
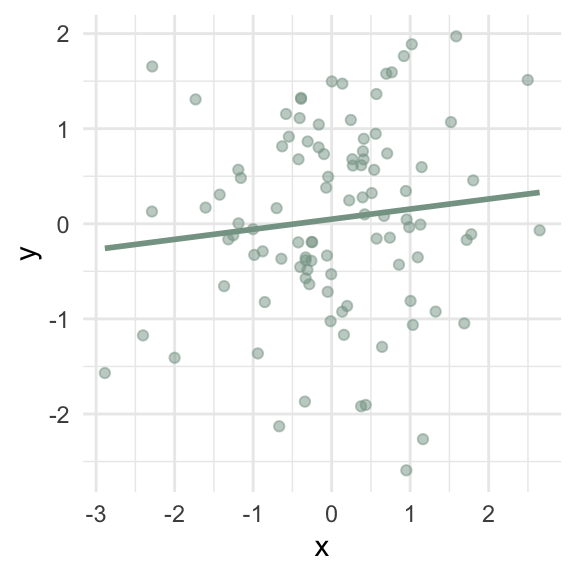
\(\hat\beta_1\) = 0.11 (95% CI: -0.08, 0.3)
How can I add the fitted values \((\hat{y})\) to my data frame?
How can I add the residual values \((e)\) to my data frame?
How can I add the residual values \((e)\) to my data frame?
How can I create a scatterplot of the residuals vs the fitted values?
How can I create a scatterplot of the residuals vs the fitted values?
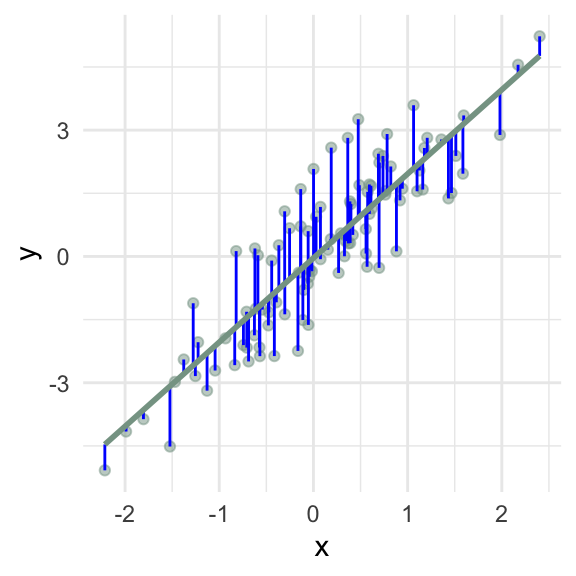
\(\sum e_i\) = 0
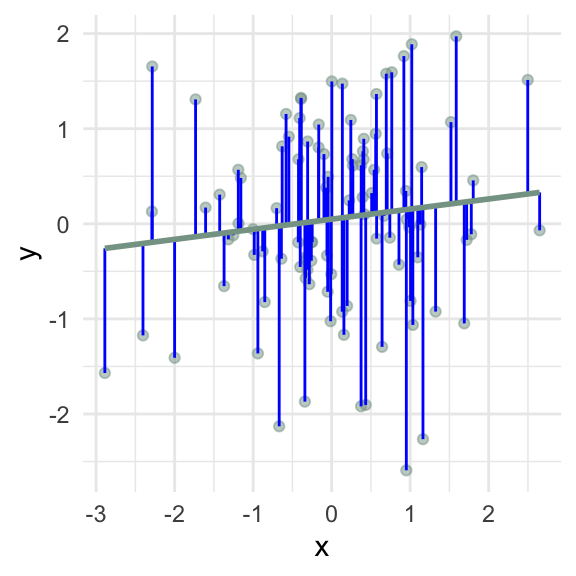
\(\sum e_i\) = 0
lm in R)How can I create a scatterplot of the residuals vs the fitted values?
d4 <- tibble(x = rnorm(100),
y = 2 * x + x / 2 * rnorm(100, sd = 10))
m4 <- lm(y ~ x, data = d4)
d4 <- d4 %>%
mutate(y_hat = fitted(m4),
e = residuals(m4))
ggplot(d4, aes(x = y_hat, y = e)) +
geom_point(color = "#86a293") +
geom_hline(yintercept = 0, color = "#86a293") +
labs(x = "Fitted value",
y = "Residual")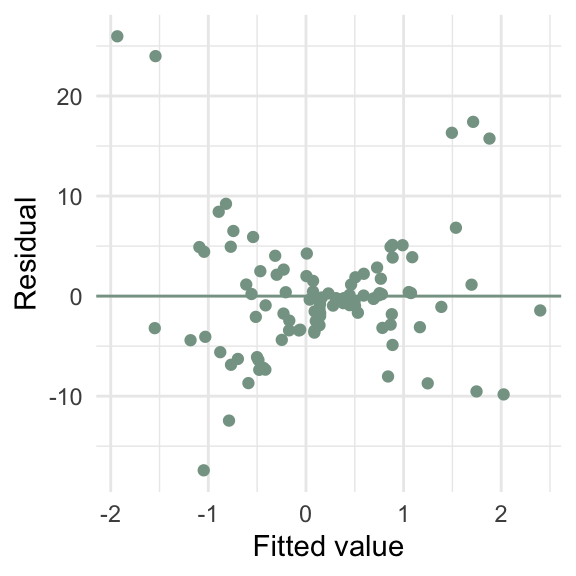
d5 <- tibble(x = runif(100, max = 10),
y = x * rnorm(100, sd = 10))
m5 <- lm(y ~ x, data = d5)
d5 <- d5 %>%
mutate(y_hat = fitted(m5),
e = residuals(m5))
ggplot(d5, aes(x = y_hat, y = e)) +
geom_point(color = "#86a293") +
geom_hline(yintercept = 0, color = "#86a293") +
labs(x = "Fitted value",
y = "Residual")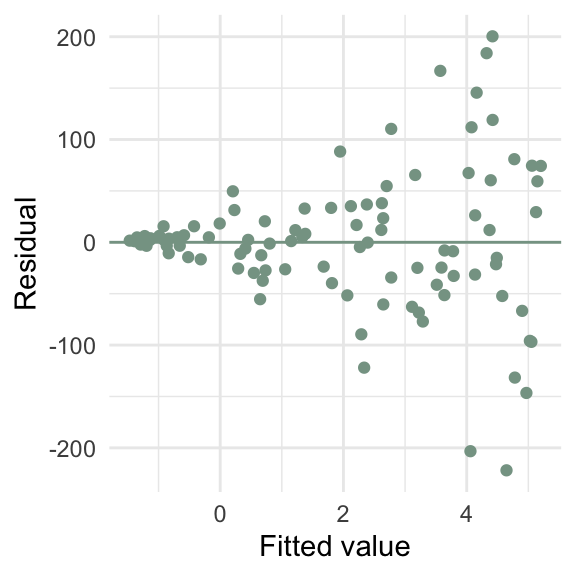
What kind of plot could help us assess whether a variable’s distribution is Normal?
full_magnolia_data %>%
nest_by(id) %>%
mutate(mod = list(lm(leaf_length ~ leaf_width, data = data))) %>%
summarise(broom::tidy(mod, conf.int = TRUE)) %>%
filter(term == "leaf_width") %>%
ggplot() +
geom_segment(aes(
x = conf.low,
xend = conf.high,
y = id,
yend = id,
color = id == 3
)) +
geom_vline(xintercept = coef(lm(leaf_length ~ leaf_width, full_magnolia_data))[2], lty = 2) +
scale_x_continuous(limits = c(-2, 4)) +
scale_color_manual(values = c("black", "cornflower blue")) +
labs(x = "Relationship between leaf length and leaf width (Slope)",
y = "Student") +
theme(legend.position = "none")full_magnolia_data %>%
nest_by(id) %>%
mutate(mod = list(lm(leaf_length ~ leaf_width, data = data))) %>%
summarise(broom::tidy(mod, conf.int = TRUE)) %>%
filter(term == "leaf_width") %>%
ggplot() +
geom_segment(aes(
x = conf.low,
xend = conf.high,
y = id,
yend = id,
color = id == 3
)) +
geom_vline(xintercept = coef(lm(leaf_length ~ leaf_width, full_magnolia_data))[2], lty = 2) +
scale_x_continuous(limits = c(-2, 4)) +
scale_color_manual(values = c("black", "cornflower blue")) +
labs(x = "Relationship between leaf length and leaf width (Slope)",
y = "Student") +
theme(legend.position = "none")full_magnolia_data %>%
nest_by(id) %>%
mutate(mod = list(lm(leaf_length ~ leaf_width, data = data))) %>%
summarise(broom::tidy(mod, conf.int = TRUE)) %>%
filter(term == "leaf_width") %>%
ggplot() +
geom_segment(aes(
x = conf.low,
xend = conf.high,
y = id,
yend = id,
color = id == 3
)) +
geom_vline(xintercept = coef(lm(leaf_length ~ leaf_width, full_magnolia_data))[2], lty = 2) +
scale_x_continuous(limits = c(-2, 4)) +
scale_color_manual(values = c("black", "cornflower blue")) +
labs(x = "Relationship between leaf length and leaf width (Slope)",
y = "Student") +
theme(legend.position = "none")Are these independent?
full_magnolia_data %>%
nest_by(id) %>%
mutate(mod = list(lm(leaf_length ~ leaf_width, data = data))) %>%
summarise(broom::tidy(mod, conf.int = TRUE)) %>%
filter(term == "leaf_width") %>%
ggplot() +
geom_segment(aes(
x = conf.low,
xend = conf.high,
y = id,
yend = id,
color = id == 3
)) +
scale_x_continuous(limits = c(-2, 4)) +
geom_vline(xintercept = coef(lm(leaf_length ~ leaf_width, full_magnolia_data))[2],
lty = 2) +
scale_color_manual(values = c("black", "cornflower blue")) +
labs(x = "Relationship between leaf length and leaf width (Slope)",
y = "Student") +
theme(legend.position = "none")Was the sample random?
avg_slope <- coef(lm(leaf_length ~ leaf_width, data = full_magnolia_data))[2]
full_magnolia_data %>%
nest_by(id) %>%
mutate(mod = list(lm(leaf_length ~ leaf_width, data = data))) %>%
summarise(broom::tidy(mod, conf.int = TRUE)) %>%
filter(term == "leaf_width") %>%
ungroup() %>%
summarise(coverage = mean(
conf.low < avg_slope &
conf.high > avg_slope
))# A tibble: 1 × 1
coverage
<dbl>
1 0.611Let’s actually randomly sample from your magnolia data
full_magnolia_data %>%
nest_by(random_id) %>%
mutate(mod = list(lm(leaf_length ~ leaf_width, data = data))) %>%
summarise(broom::tidy(mod, conf.int = TRUE)) %>%
filter(term == "leaf_width") %>%
ggplot() +
geom_segment(aes(
x = conf.low,
xend = conf.high,
y = random_id,
yend = random_id,
color = random_id == 3
)) +
geom_vline(xintercept = coef(lm(leaf_length ~ leaf_width, full_magnolia_data))[2], lty = 2) +
scale_x_continuous(limits = c(-2, 4)) +
scale_color_manual(values = c("black", "cornflower blue")) +
labs(x = "Relationship between leaf length and leaf width (Slope)",
y = "Student") +
theme(legend.position = "none")# A tibble: 1 × 1
coverage
<dbl>
1 0.909