Hypothesis Testing and P-values
Lucy D’Agostino McGowan
Application Exercise
- Copy the following template into RStudio Pro:
- Go to https://lucy.shinyapps.io/magnolia-data/ and collect 30 data points
- Bring your data into R. Fit a linear model predicting leaf length from leaf width
- What is the coefficient for \(\hat\beta_1\)? What is the t-statistic? What is the p-value?
- What hypothesis is this p-value assessing?
Hypothesis testing
- Null hypothesis: \(\beta_1 = 0\)
- Alternative hypothesis: \(\beta_1 \neq 0\)
Under the null hypothesis
Under the null \((\beta_1 = 0)\) the t-statistic \((\hat\beta_1/se_{\hat\beta_1})\) has a t-distribution with \(n-2\) degrees of freedom.
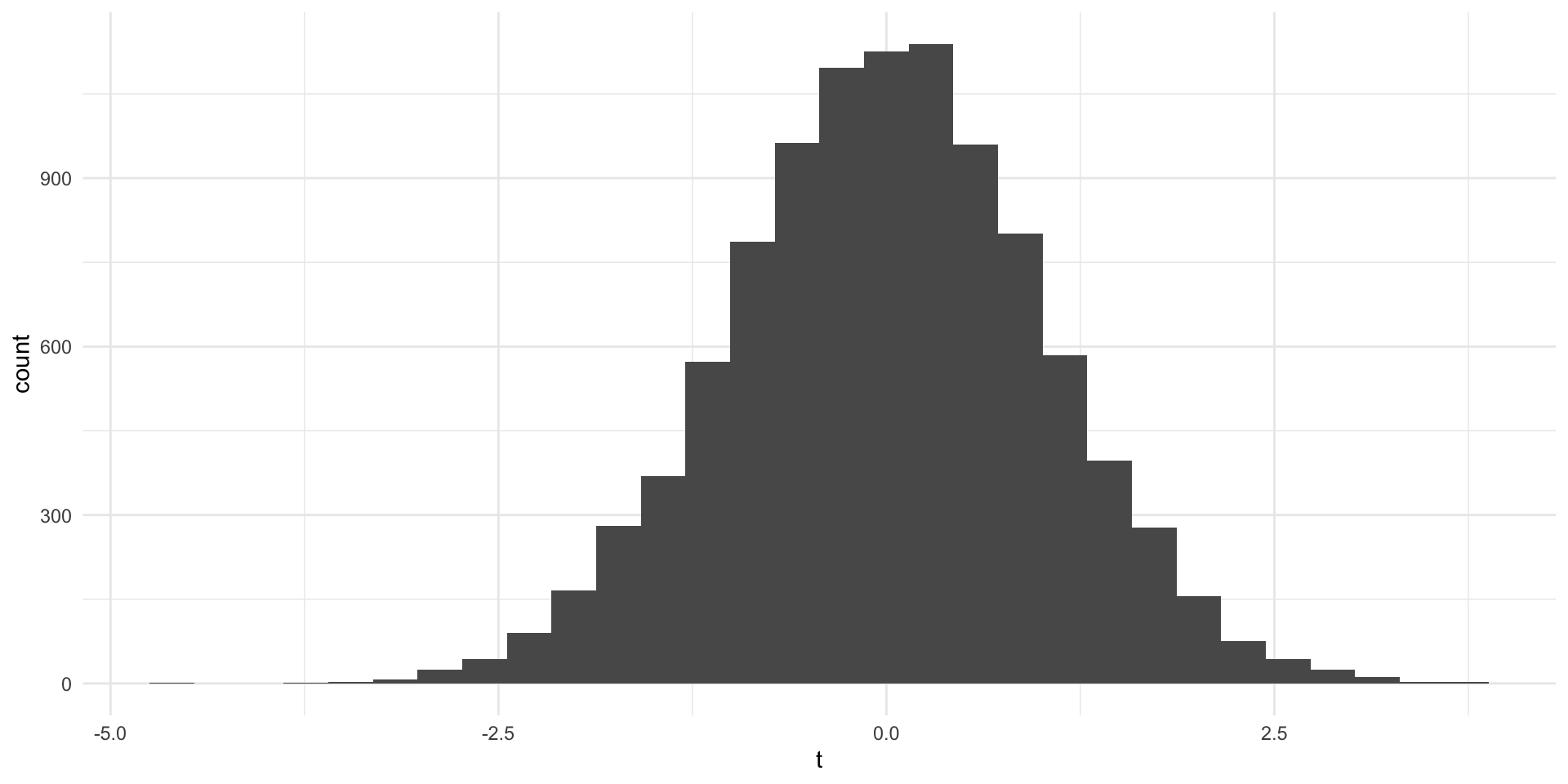
Example
What t statistic did we observe?
Call:
lm(formula = leaf_length ~ leaf_width, data = magnolia_data)
Residuals:
Min 1Q Median 3Q Max
-12.4544 -3.2196 -0.0287 3.1761 12.6086
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.8362 1.3956 8.481 2.36e-13 ***
leaf_width 0.4386 0.1552 2.826 0.00571 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.327 on 98 degrees of freedom
Multiple R-squared: 0.07537, Adjusted R-squared: 0.06593
F-statistic: 7.988 on 1 and 98 DF, p-value: 0.005707Under the Null Hypothesis
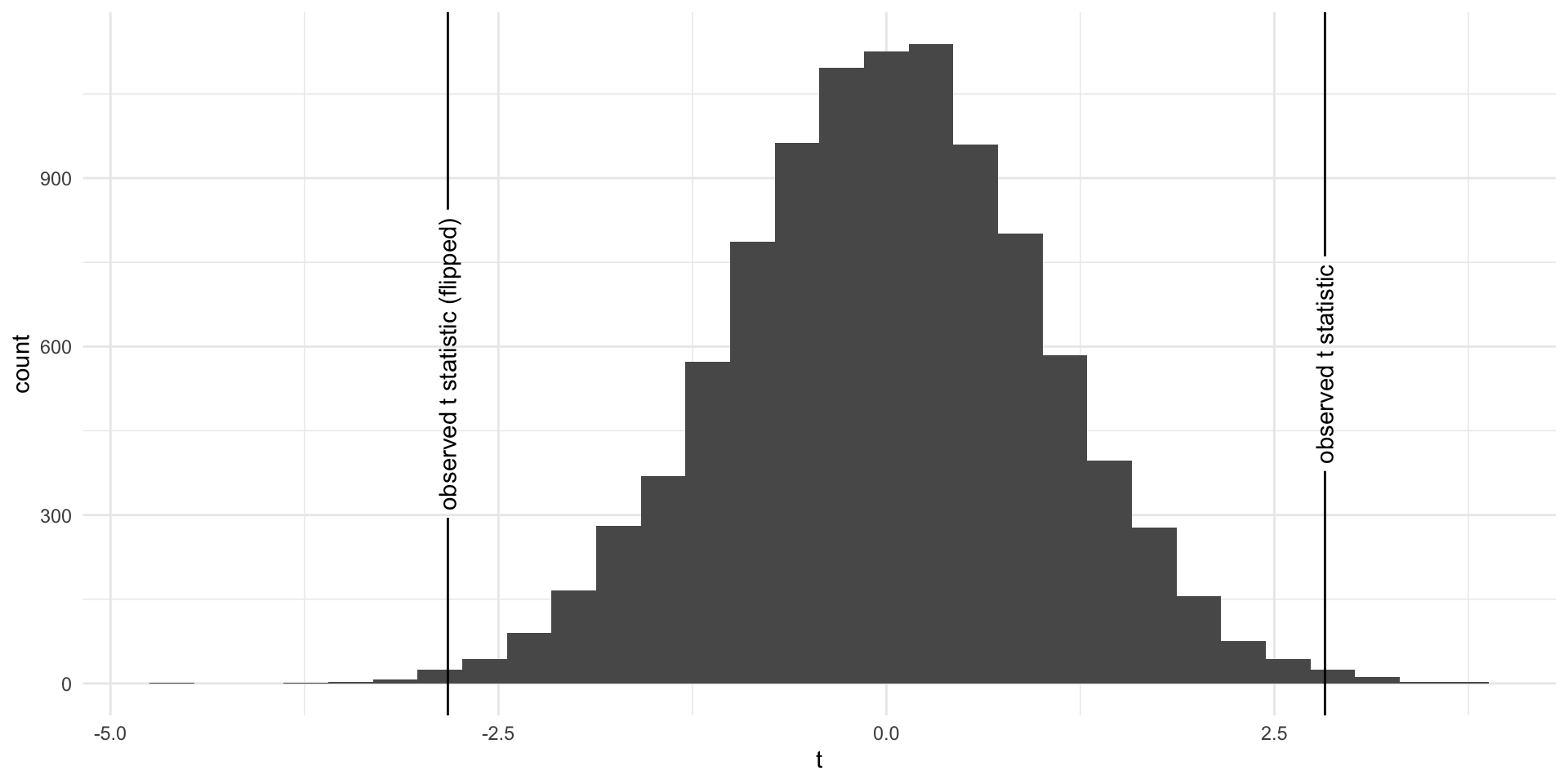
- How do we compare these to the distribution under the null?
p-value
The probability of observing a statistic as extreme or more extreme than the observed test statistic given the null hypothesis is true
Under the Null Hypothesis
Code
null$color <- ifelse(null$t < 2.826 & null$t > -2.826, "out", "in")
ggplot(null, aes(t, fill = color)) +
geom_histogram(bins = 30) +
geom_textvline(xintercept = c(2.826), label = "observed t statistic") +
geom_textvline(xintercept = c(-2.826), label = "observed t statistic (flipped)") +
theme(legend.position = "none")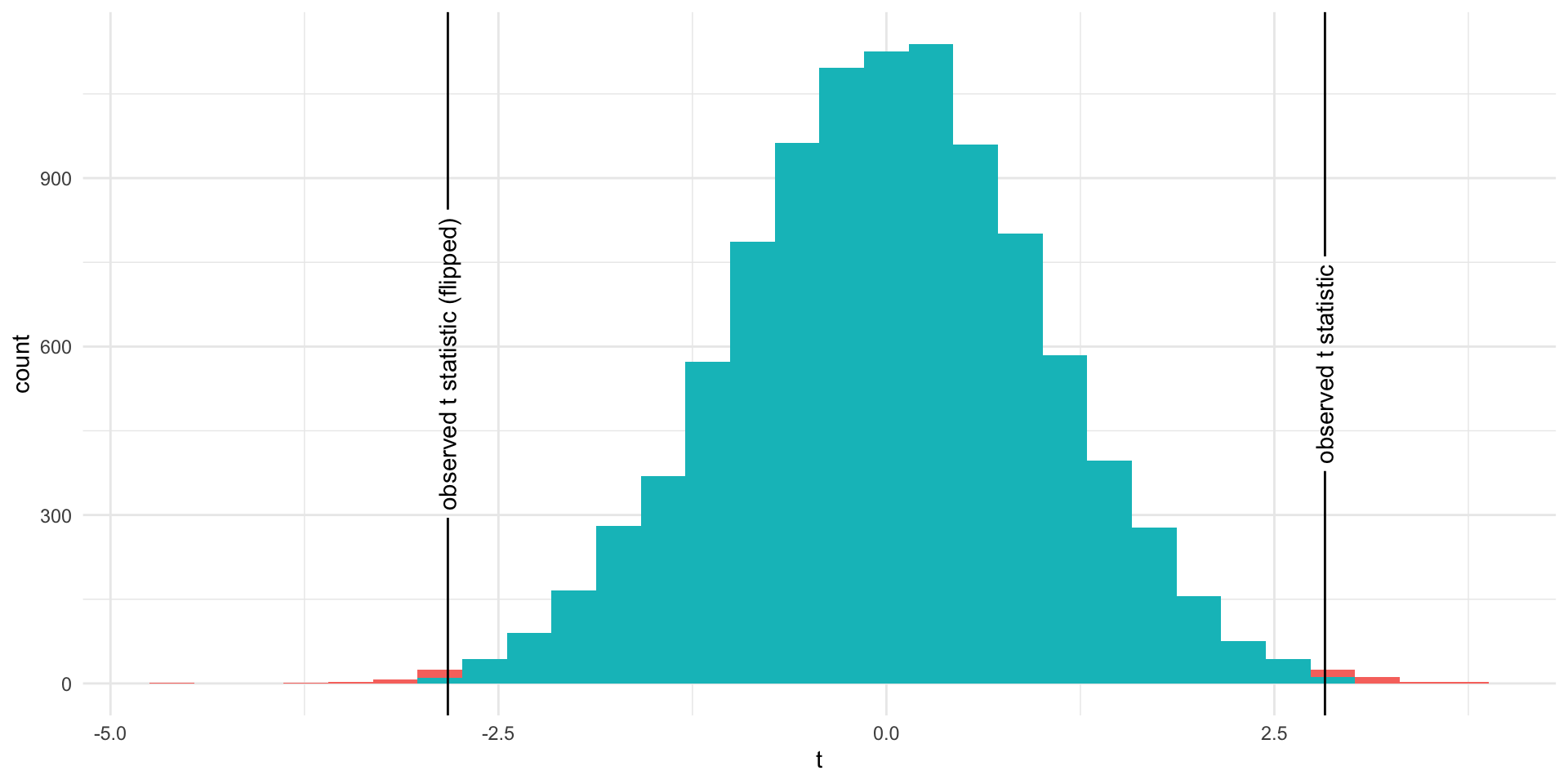
Under the Null Hypothesis
The proportion of area greater than 2.826
Code
null$color <- ifelse(null$t < 2.826 & null$t > -2.826, "out", "in")
ggplot(null, aes(t, fill = color)) +
geom_histogram(bins = 30) +
geom_textvline(xintercept = c(2.826), label = "observed t statistic") +
geom_textvline(xintercept = c(-2.826), label = "observed t statistic (flipped)") +
theme(legend.position = "none")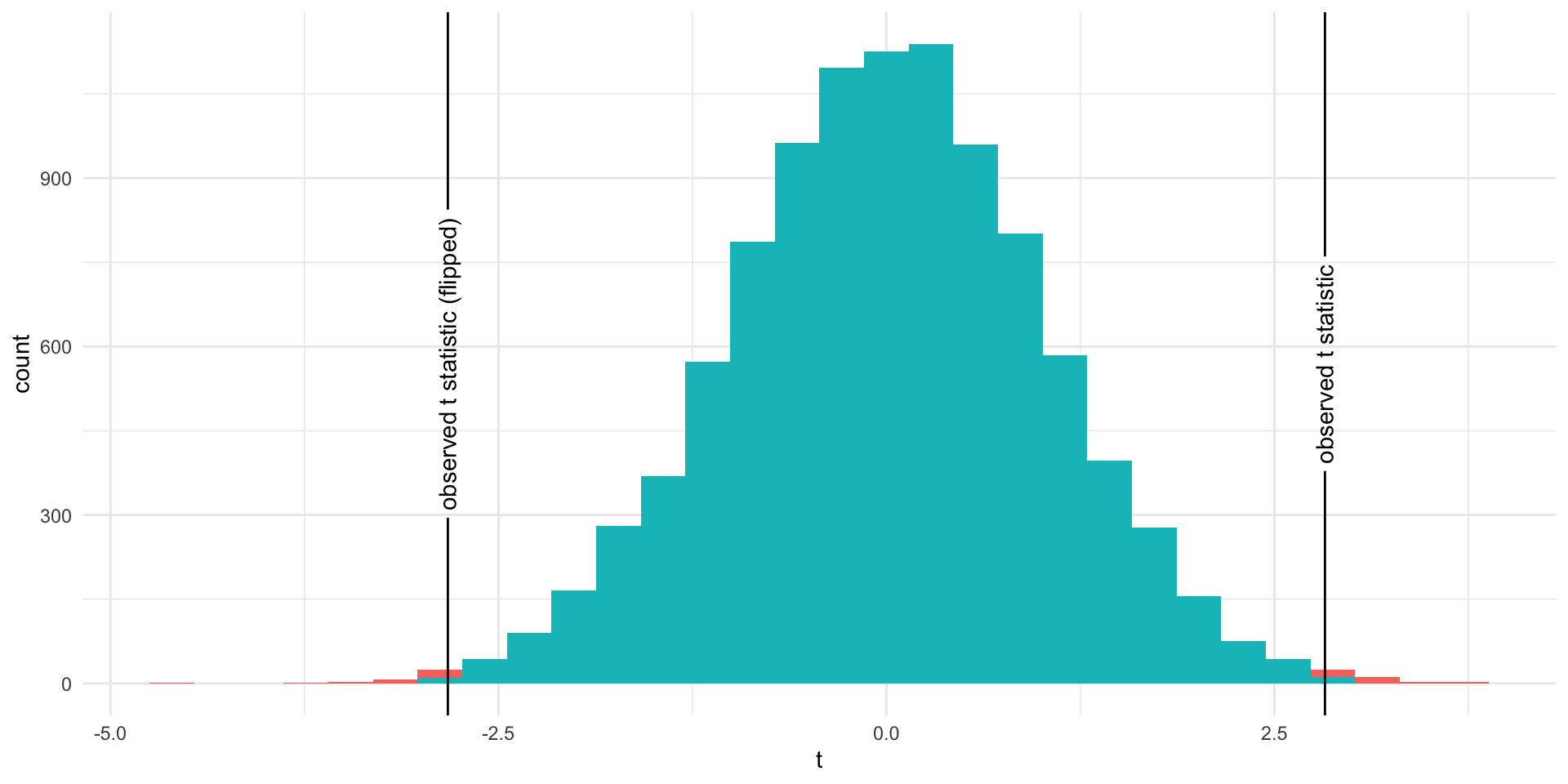
Under the Null Hypothesis
The proportion of area less than -2.826
Code
null$color <- ifelse(null$t < 2.826 & null$t > -2.826, "out", "in")
ggplot(null, aes(t, fill = color)) +
geom_histogram(bins = 30) +
geom_textvline(xintercept = c(2.826), label = "observed t statistic") +
geom_textvline(xintercept = c(-2.826), label = "observed t statistic (flipped)") +
theme(legend.position = "none")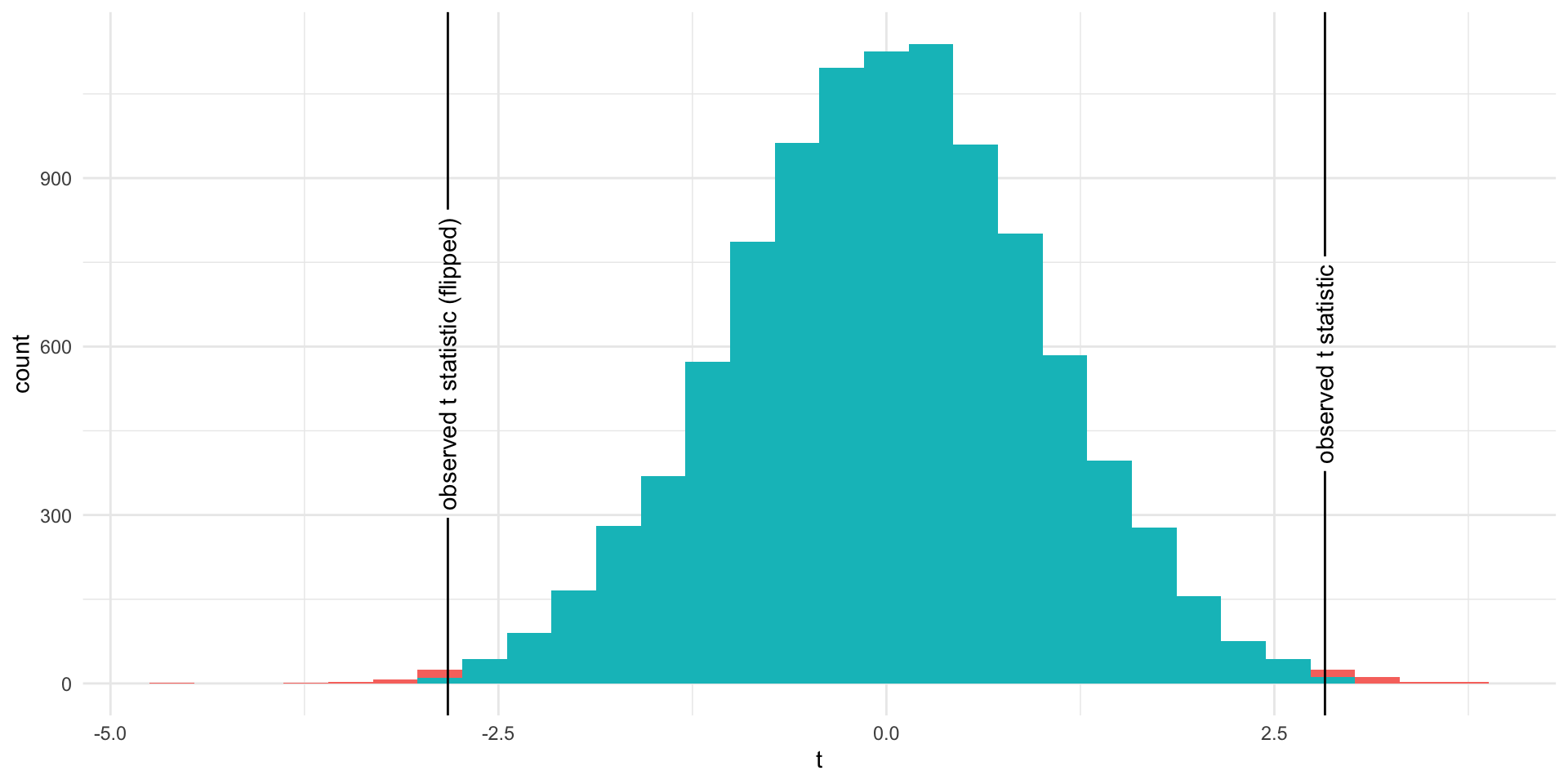
Under the Null Hypothesis
The proportion of area greater than 2.826 or less than -2.826
Code
null$color <- ifelse(null$t < 2.826 & null$t > -2.826, "out", "in")
ggplot(null, aes(t, fill = color)) +
geom_histogram(bins = 30) +
geom_textvline(xintercept = c(2.826), label = "observed t statistic") +
geom_textvline(xintercept = c(-2.826), label = "observed t statistic (flipped)") +
theme(legend.position = "none")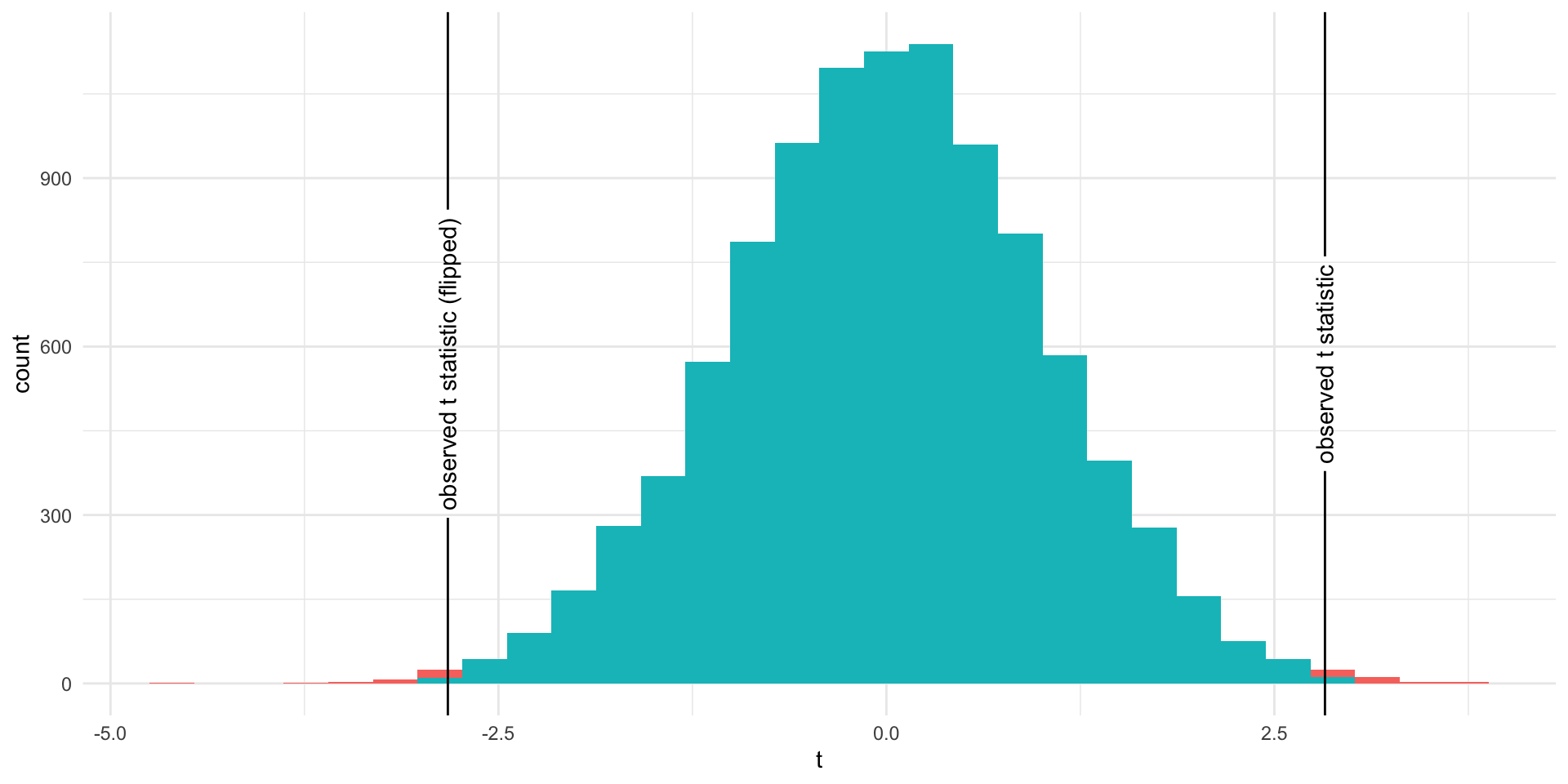
Under the Null Hypothesis
The proportion of area greater than 2.826 or less than -2.826
Code
null$color <- ifelse(null$t < 2.826 & null$t > -2.826, "out", "in")
ggplot(null, aes(t, fill = color)) +
geom_histogram(bins = 30) +
geom_textvline(xintercept = c(2.826), label = "observed t statistic") +
geom_textvline(xintercept = c(-2.826), label = "observed t statistic (flipped)") +
theme(legend.position = "none")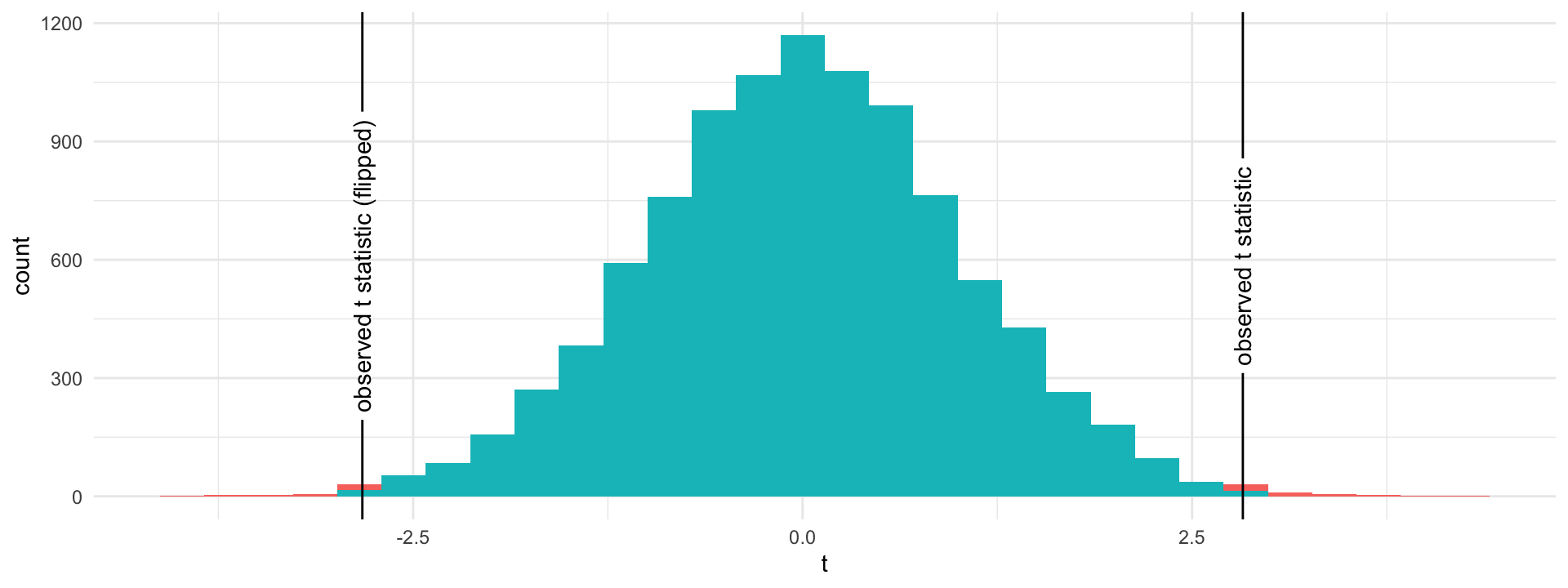
![]()