Evaluating Multiple Linear Regression Models

Lucy D’Agostino McGowan

Conditions for multiple linear regression

Assumption What it means How do you check? How do you fix?
Linearity The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant Residuals vs. fits plot
Marginal effects plots		 fit a better model (transformations, polynomial terms, more / different variables, etc.)

Conditions for multiple linear regression

Assumption What it means How do you check? How do you fix?
Linearity The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant Residuals vs. fits plot
Marginal effects plots		 fit a better model (transformations, polynomial terms, more / different variables, etc.)

Transforming the outcome variable

  • So far, we’ve talked about transforming an explanatory variable (for example including polynomial terms)
  • It is common to transform the outcome variable by taking the log or the square root of the outcome. This is particularly useful for constant variance violations
  • You need to be careful when interpreting coefficients after taking transformations, as the transformation needs to be accounted for (now a \(\hat\beta\) is a one unit change in x yields an expected change in the log of y, for example)

Conditions for multiple linear regression

Assumption What it means How do you check? How do you fix?
Linearity The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant Residuals vs. fits plot
Marginal effects plots		 fit a better model (transformations, polynomial terms, more / different variables, etc.)

Marginal effects plots

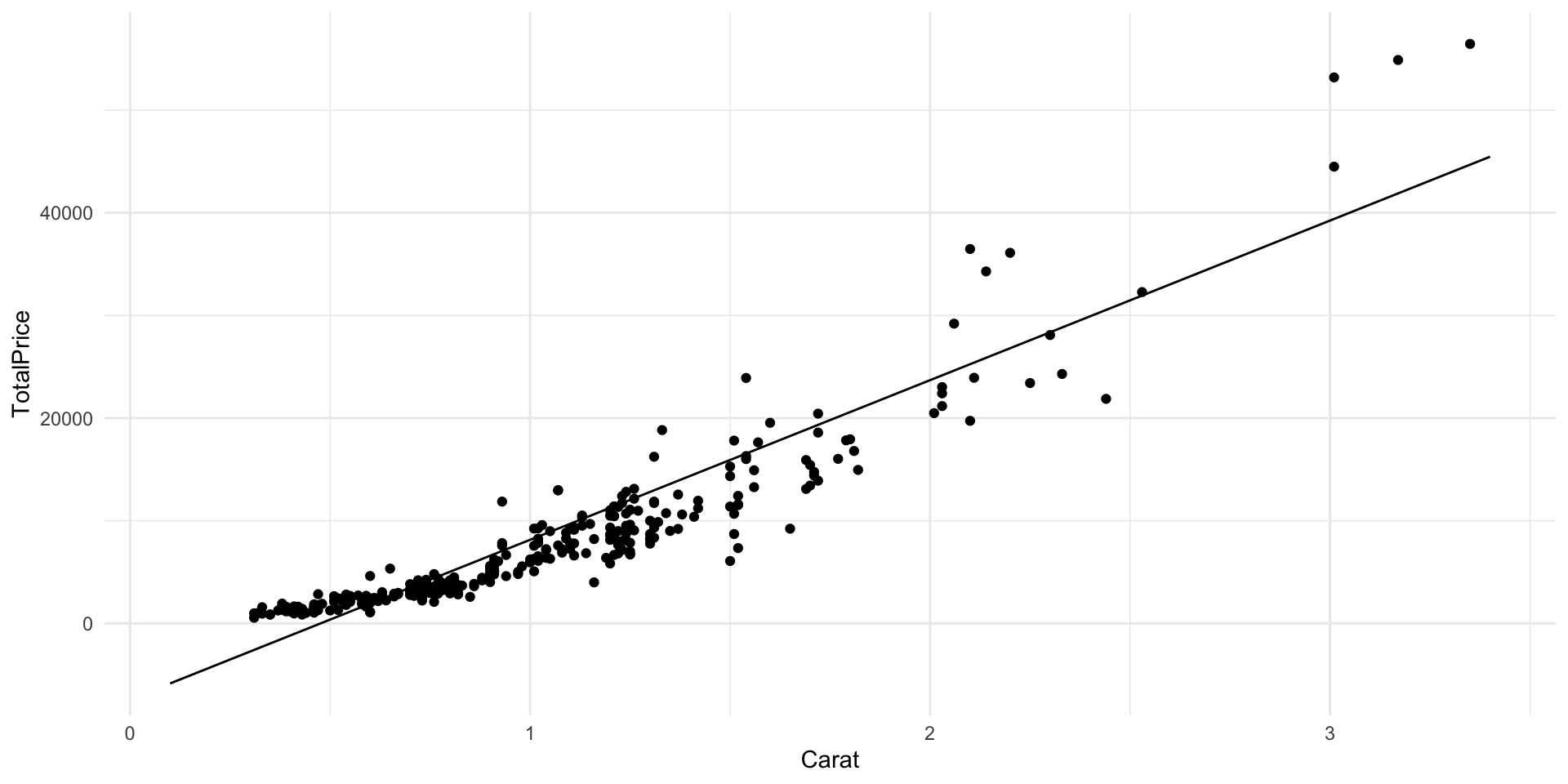
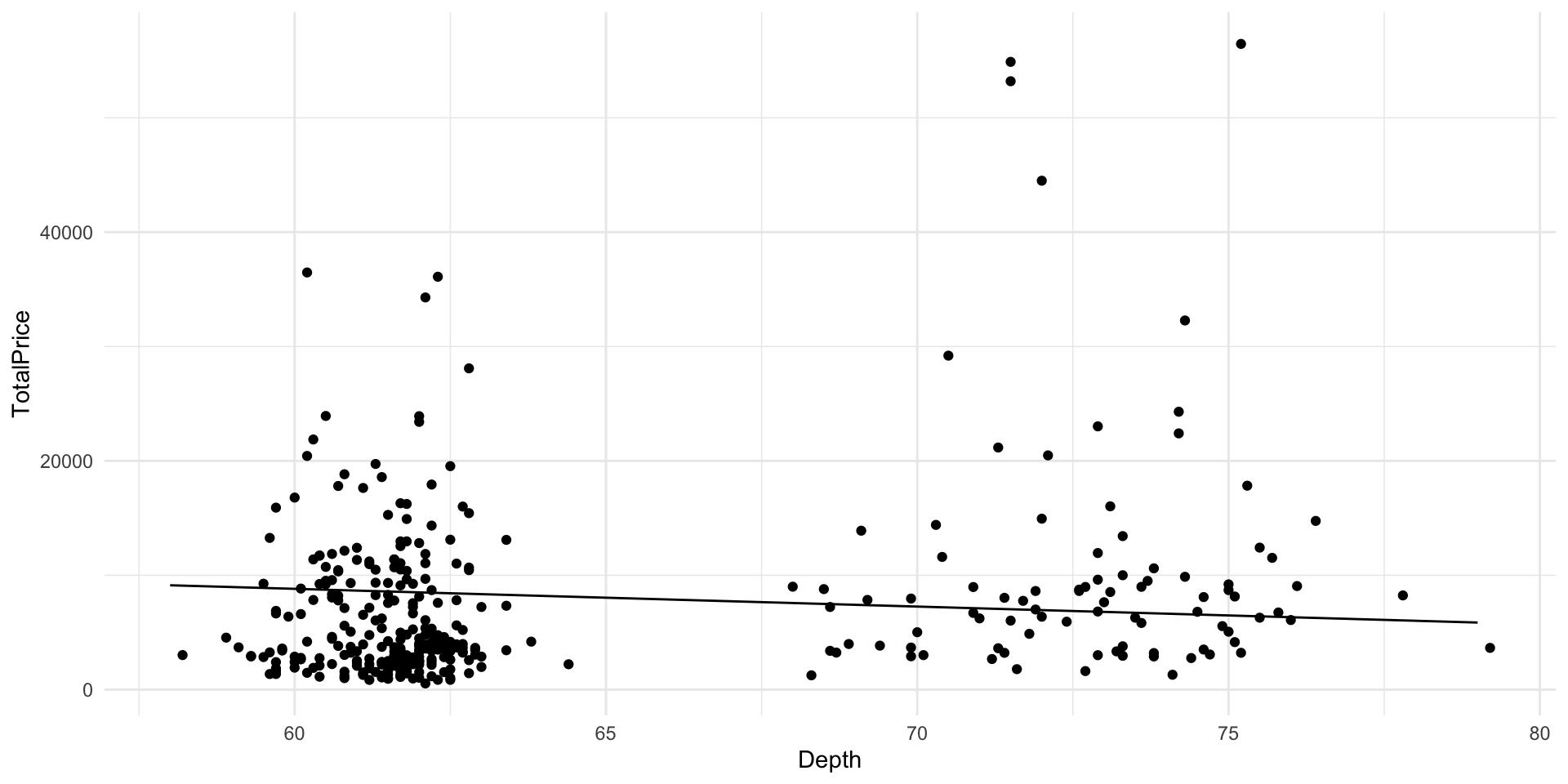
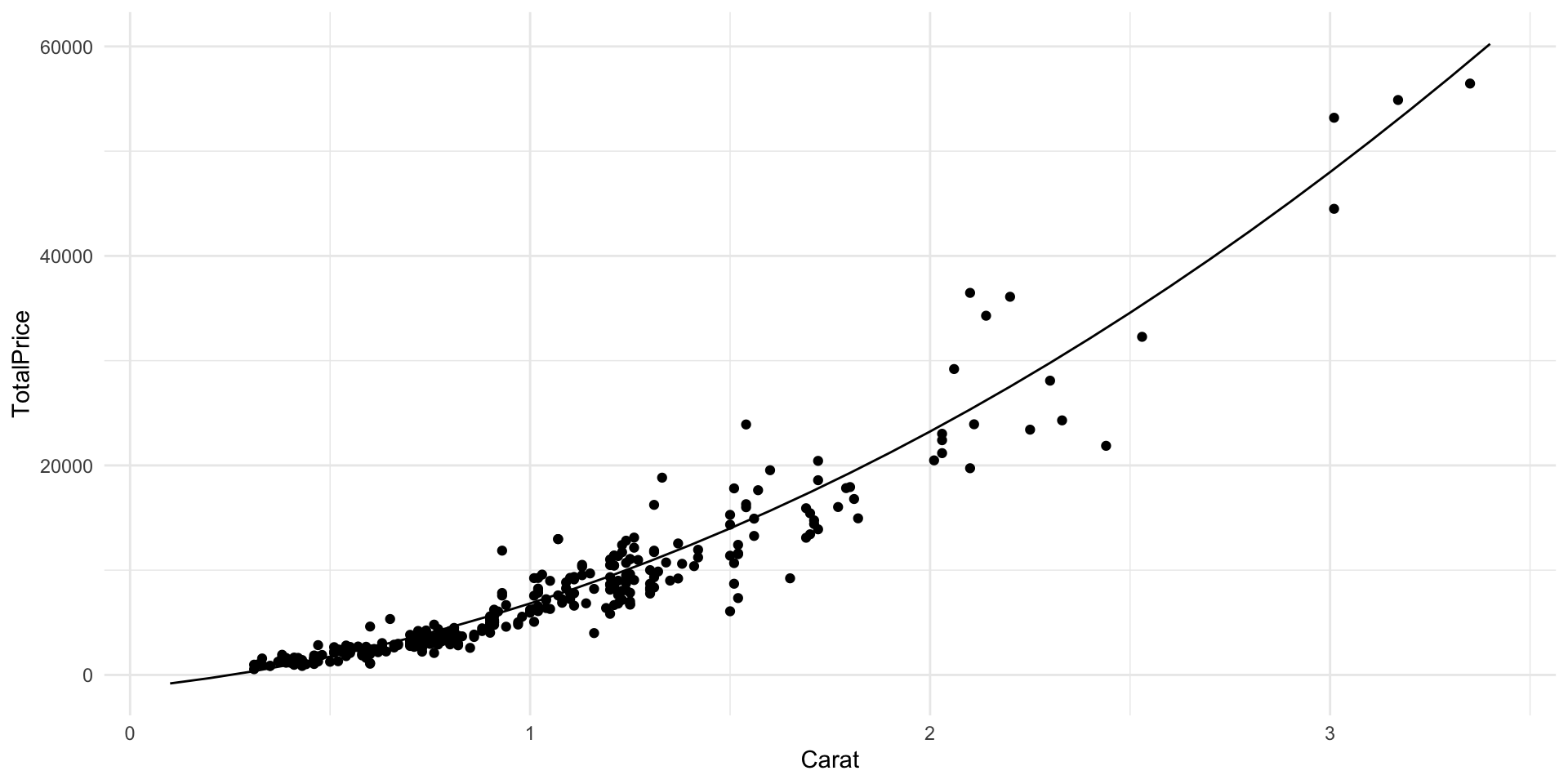
  • When we did simple linear regression we could examine a scatter plot of \(x\) and \(y\), but how can we do this when we have multiple explanatory variables in our model?
  • One option is to predict new values of \(\hat{y}\) over a range of a particlar \(x\) variable, holding all other variables at their reference values for categorical variables and the average value for continuous variables.

Marginal effect plots

library(Stat2Data)
data("Diamonds")

mod <- lm(TotalPrice ~ Carat + Depth + Color, data = Diamonds)

Diamonds %>%
  mutate(y_hat = fitted(mod),
         resid = residuals(mod)) %>%
  ggplot(aes(x = y_hat, y = resid)) +
  geom_point() +
  geom_hline(yintercept = 0) + 
  labs(x = "Fitted values", y = "Residuals")

Marginal effect plots

new_data <- data.frame(
  Carat = seq(.1, 3.4, by = 0.1),
  Depth = mean(Diamonds$Depth),
  Color = "D"
)

ggplot(Diamonds, aes(x = Carat, y = TotalPrice)) +
  geom_point() +
  geom_line(data = new_data, aes(x = Carat, y = predict(mod, new_data))) 

new_data2 <- data.frame(
  Carat = mean(Diamonds$Carat),
  Depth = seq(58, 79, by = 1),
  Color = "D"
)

ggplot(Diamonds, aes(x = Depth, y = TotalPrice)) +
  geom_point() +
  geom_line(data = new_data2, aes(x = Depth, y = predict(mod, new_data2)))

Marginal effect plots

mod2 <- lm(TotalPrice ~ Carat + I(Carat^2) + Depth + Color, data = Diamonds)

ggplot(Diamonds, aes(x = Carat, y = TotalPrice)) +
  geom_point() +
  geom_line(data = new_data, aes(x = Carat, y = predict(mod2, new_data)))

Conditions for multiple linear regression

Assumption What it means How do you check? How do you fix?
Linearity The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant Residuals vs. fits plot
Marginal effects plots		 fit a better model (transformations, polynomial terms, more / different variables, etc.)
Zero Mean

Conditions for multiple linear regression

Assumption What it means How do you check? How do you fix?
Linearity The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant Residuals vs. fits plot
Marginal effects plots		 fit a better model (transformations, polynomial terms, more / different variables, etc.)
Zero Mean The error distribution is centered at zero by default –
Constant Variance

Conditions for multiple linear regression

Assumption What it means How do you check? How do you fix?
Linearity The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant Residuals vs. fits plot
Marginal effects plots		 fit a better model (transformations, polynomial terms, more / different variables, etc.)
Zero Mean The error distribution is centered at zero by default –
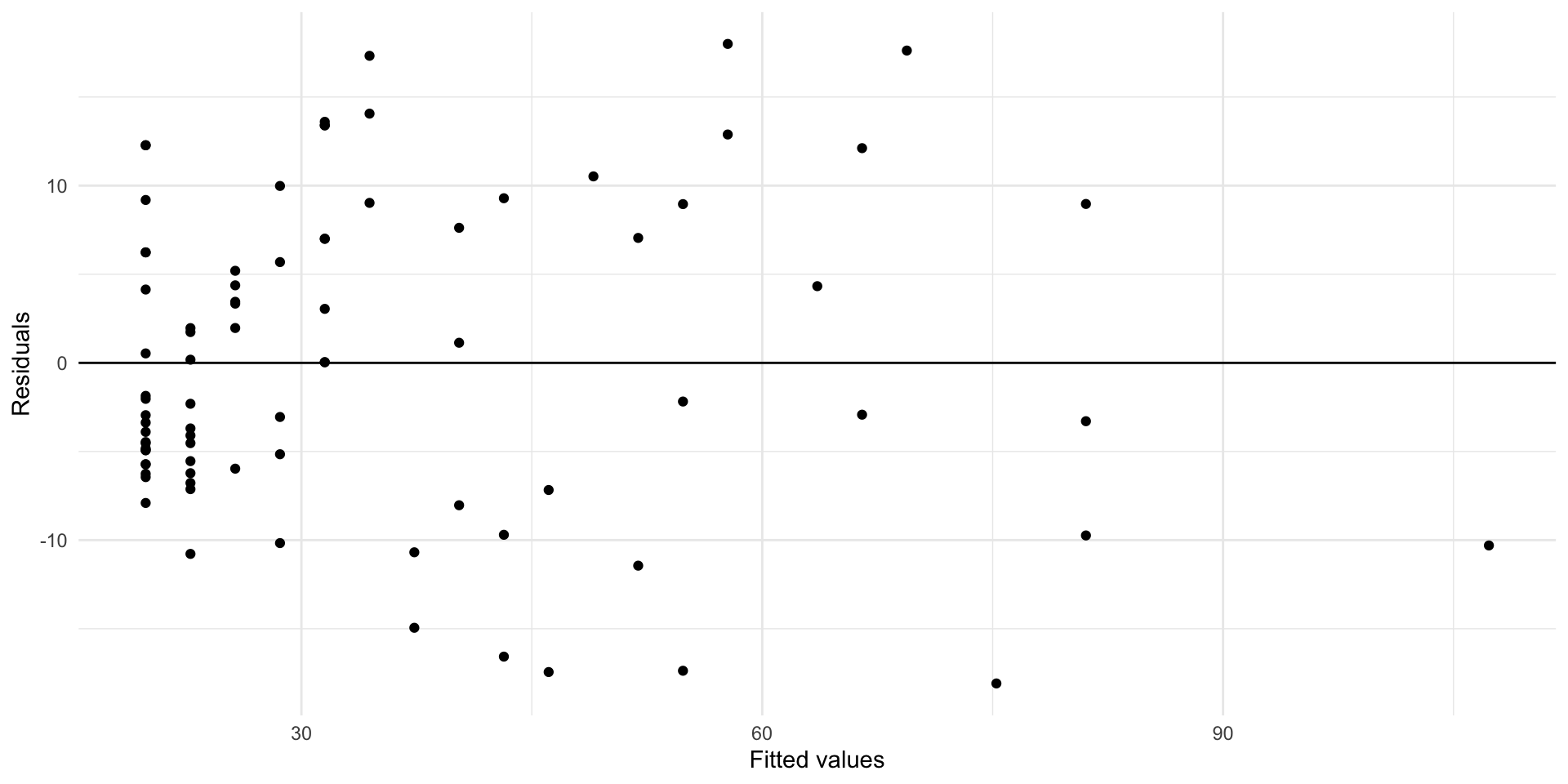
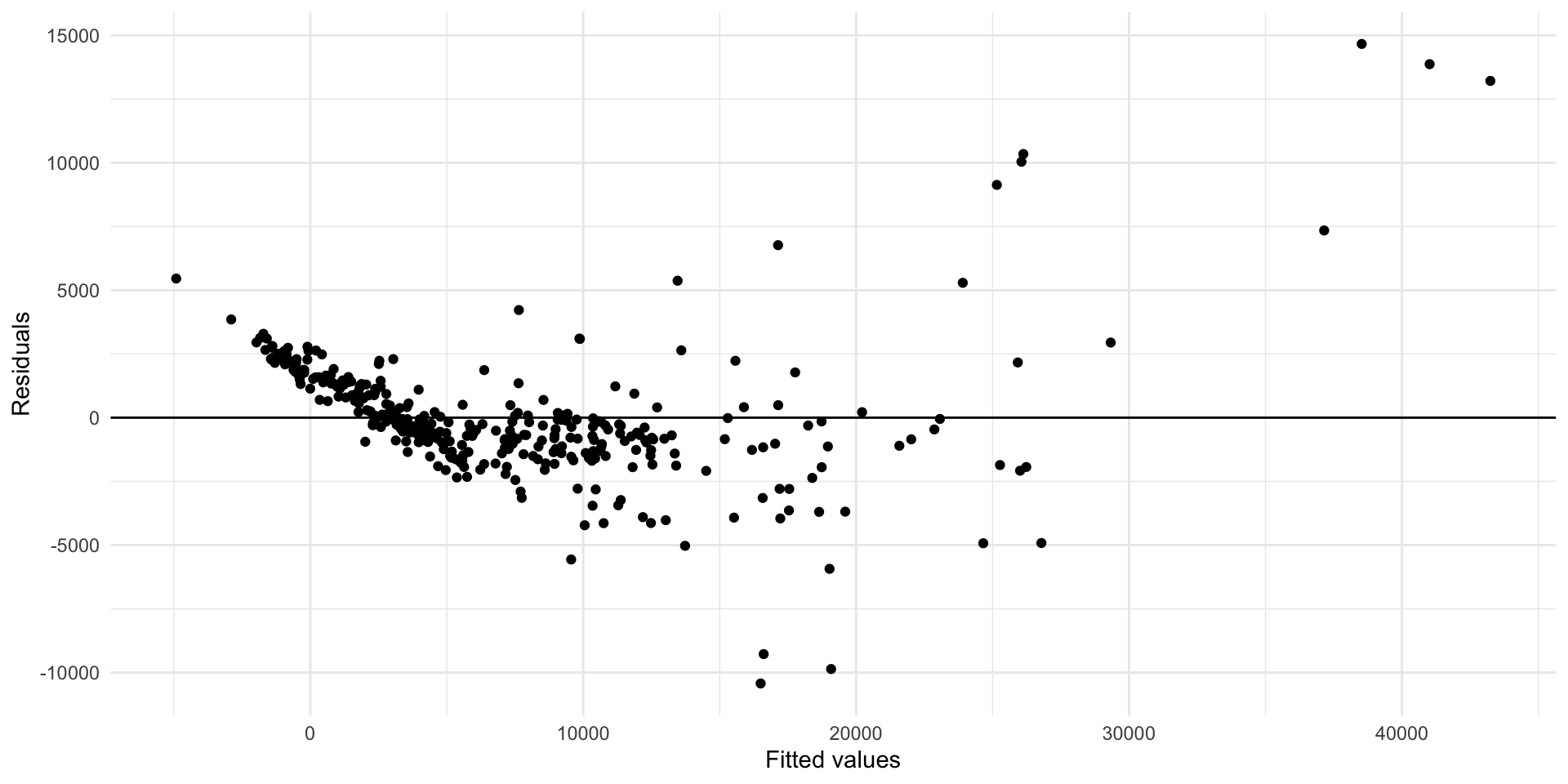
Constant Variance The variability in the errors is the same for all values of the predictor variable Residuals vs fits plot fit a better model (try taking the log or square root of the outcome)
Independence

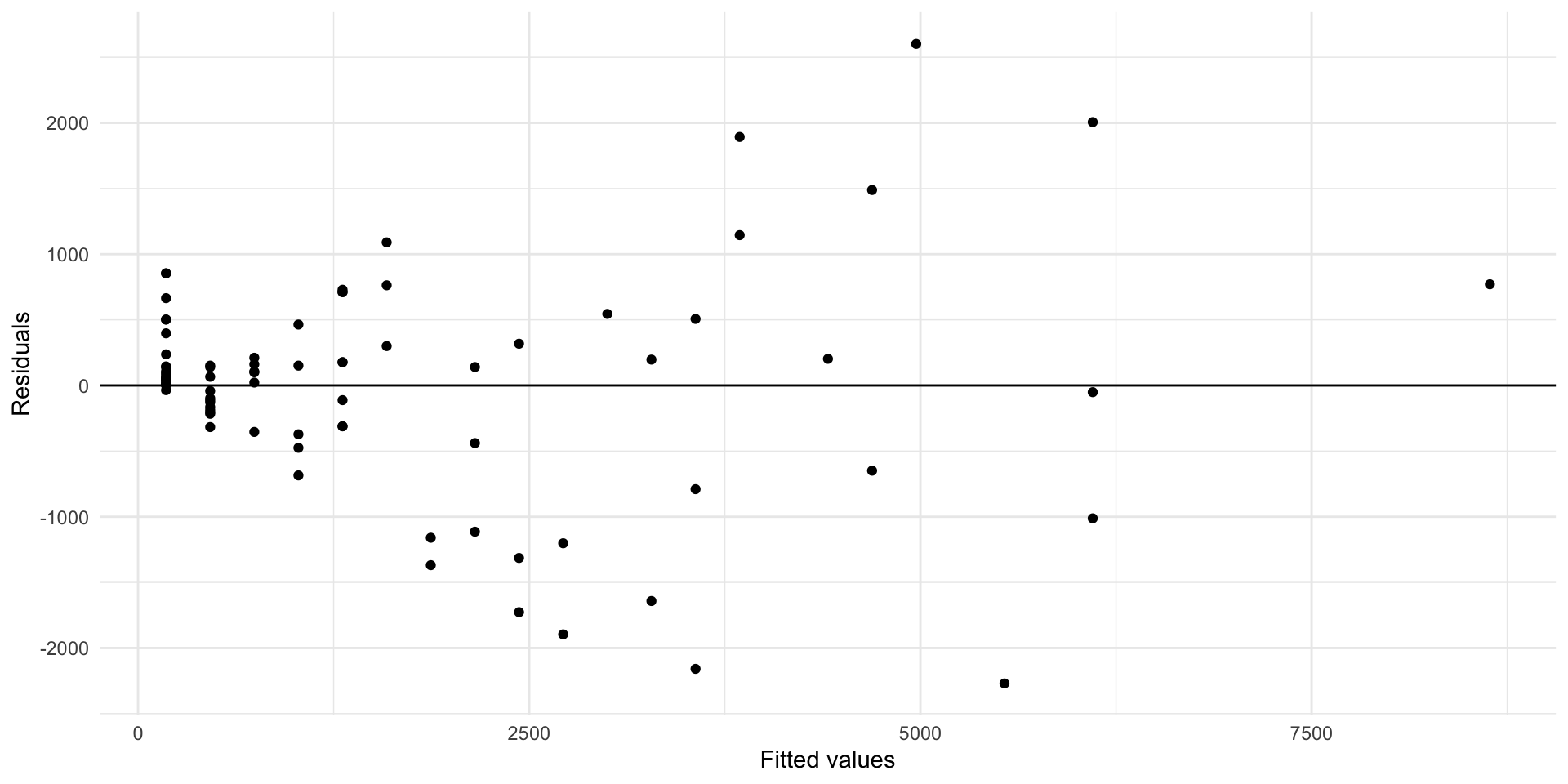
Transformation of y example

data("MetroHealth83")

mod <- lm(NumMDs ~ NumHospitals, data = MetroHealth83)
MetroHealth83 %>%
  mutate(y_hat = fitted(mod),
         resid = residuals(mod)) %>%
  ggplot(aes(x = y_hat, y = resid)) +
  geom_point() +
  geom_hline(yintercept = 0) + 
  labs(x = "Fitted values", y = "Residuals")

Transformation of y example

Try taking the log of the outcome.

mod2 <- lm(log(NumMDs) ~ NumHospitals, data = MetroHealth83)
Code 
MetroHealth83 %>%
  mutate(y_hat = fitted(mod2),
         resid = residuals(mod2)) %>%
  ggplot(aes(x = y_hat, y = resid)) +
  geom_point() +
  geom_hline(yintercept = 0) + 
  labs(x = "Fitted values", y = "Residuals")

Transformation of y example

Try taking the log of the outcome.

mod2 <- lm(log(NumMDs) ~ NumHospitals, data = MetroHealth83)
summary(mod2)

Call:
lm(formula = log(NumMDs) ~ NumHospitals, data = MetroHealth83)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.24906 -0.55027 -0.03063  0.49255  1.11936 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   5.75892    0.10046   57.32   <2e-16 ***
NumHospitals  0.14499    0.01047   13.84   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6054 on 81 degrees of freedom
Multiple R-squared:  0.7029,    Adjusted R-squared:  0.6992 
F-statistic: 191.6 on 1 and 81 DF,  p-value: < 2.2e-16

How do you interpret \(\hat\beta_1\)?

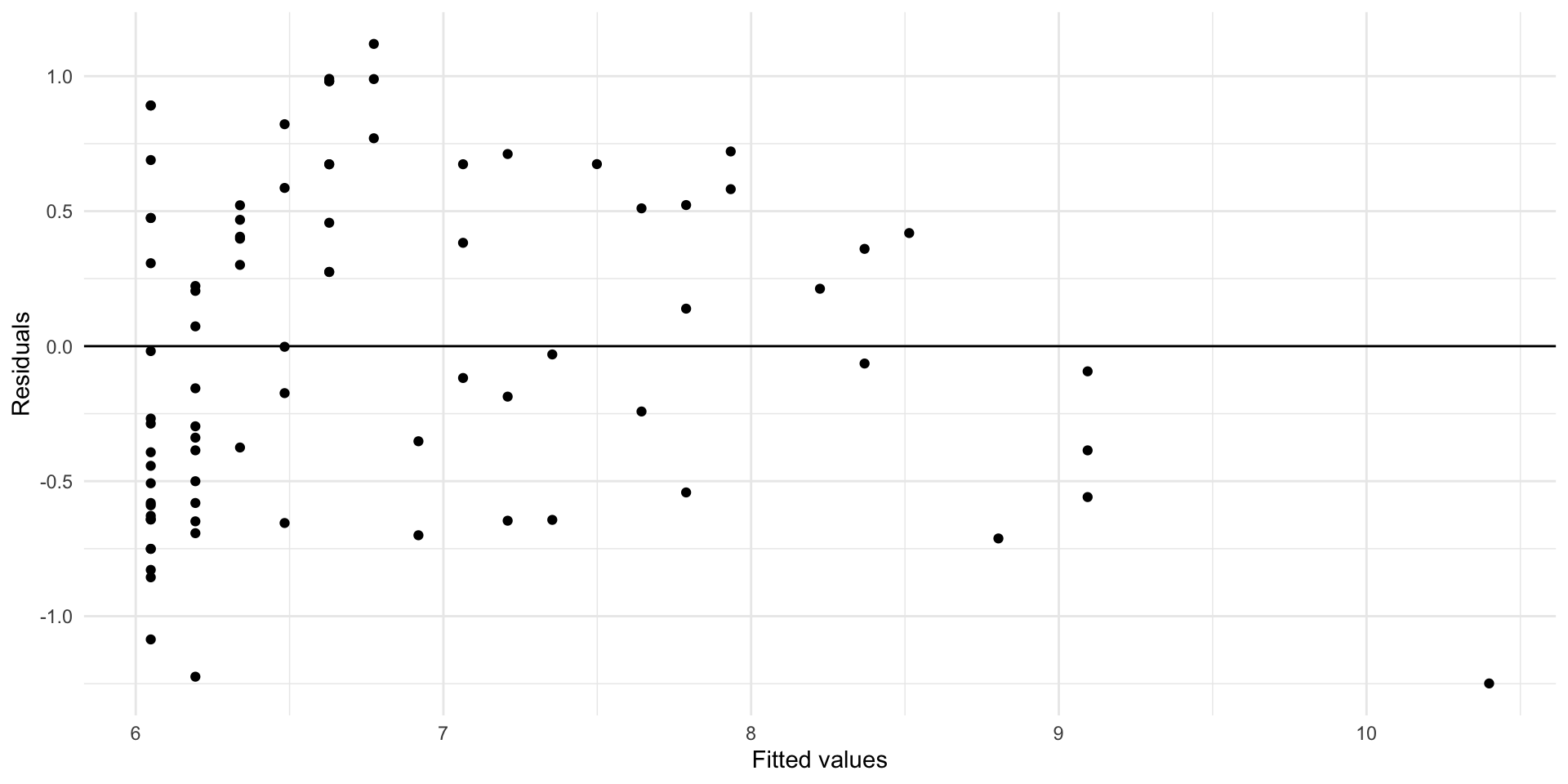
Transformation of y example

Try taking the square root of the outcome.

mod3 <- lm(sqrt(NumMDs) ~ NumHospitals, data = MetroHealth83)
Code 
MetroHealth83 %>%
  mutate(y_hat = fitted(mod3),
         resid = residuals(mod3)) %>%
  ggplot(aes(x = y_hat, y = resid)) +
  geom_point() +
  geom_hline(yintercept = 0) + 
  labs(x = "Fitted values", y = "Residuals")

Transformation of y example

Try taking the square root of the outcome.

mod3 <- lm(sqrt(NumMDs) ~ NumHospitals, data = MetroHealth83)
summary(mod3)

Call:
lm(formula = sqrt(NumMDs) ~ NumHospitals, data = MetroHealth83)

Residuals:
    Min      1Q  Median      3Q     Max 
-18.086  -5.845  -2.030   7.001  17.994 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   14.0329     1.4686   9.555 6.36e-15 ***
NumHospitals   2.9148     0.1531  19.036  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.85 on 81 degrees of freedom
Multiple R-squared:  0.8173,    Adjusted R-squared:  0.8151 
F-statistic: 362.4 on 1 and 81 DF,  p-value: < 2.2e-16

How do you interpret \(\hat\beta_1\)?

Conditions for multiple linear regression

Assumption What it means How do you check? How do you fix?
Linearity The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant Residuals vs. fits plot
Marginal effects plots		 fit a better model (transformations, polynomial terms, more / different variables, etc.)
Zero Mean The error distribution is centered at zero by default –
Constant Variance The variability in the errors is the same for all values of the predictor variable Residuals vs fits plot fit a better model (try taking the log or square root of the outcome)
Independence The errors are assumed to be independent from one another 👀 data generation Find better data or fit a fancier model
Random

Conditions for multiple linear regression

Assumption What it means How do you check? How do you fix?
Linearity The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant Residuals vs. fits plot
Marginal effects plots		 fit a better model (transformations, polynomial terms, more / different variables, etc.)
Zero Mean The error distribution is centered at zero by default –
Constant Variance The variability in the errors is the same for all values of the predictor variable Residuals vs fits plot fit a better model (try taking the log or square root of the outcome)
Independence The errors are assumed to be independent from one another 👀 data generation Find better data or fit a fancier model
Random The data are obtained using a random process 👀 data generation Find better data
Normality

Conditions for multiple linear regression

Assumption What it means How do you check? How do you fix?
Linearity The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant Residuals vs. fits plot
Marginal effects plots		 fit a better model (transformations, polynomial terms, more / different variables, etc.)
Zero Mean The error distribution is centered at zero by default –
Constant Variance The variability in the errors is the same for all values of the predictor variable Residuals vs fits plot fit a better model (try taking the log or square root of the outcome)
Independence The errors are assumed to be independent from one another 👀 data generation Find better data or fit a fancier model
Random The data are obtained using a random process 👀 data generation Find better data
Normality The random errors follow a normal distribution QQ-plot / residual histogram fit a better model

Dr. Lucy D’Agostino McGowan