Logistic Regression

Lucy D’Agostino McGowan

Outcome variable

  • So far, we’ve only had continuous (numeric, quantitative) outcome variables ( \(y\) )
  • We’ve just learned about categorical and binary explanatory variables ( \(x\) )
  • What if we have a binary outcome variable?

Outcome variable

What does it mean to be a binary variable?

  • So far, we’ve only had continuous (numeric, quantitative) outcome variables ( \(y\) )
  • We’ve just learned about categorical and binary explanatory variables ( \(x\) )
  • What if we have a binary outcome variable?

Let’s look at an example

  • 446 teens were asked “On an average school night, do you get at least 7 hours of sleep”
  • Outcome is [1 = “Yes”, 0 = “No”]
  • Is Age related to this outcome?
  • What if I try to fit this as a linear regression model?
Code 
data("LosingSleep")

ggplot(LosingSleep, aes(Age, Outcome)) + 
  geom_point() + 
  geom_line(aes(x = Age, y = predict(lm(Outcome ~ Age, data = LosingSleep))))

Let’s look at an example

  • 446 teens were asked “On an average school night, do you get at least 7 hours of sleep”
  • Outcome is [1 = “Yes”, 0 = “No”]
  • Is Age related to this outcome?
  • What if I try to fit this as a linear regression model?
Code 
LosingSleep %>%
  group_by(Age) %>%
  count(Age, Outcome) %>%
  mutate(p = n / sum(n)) %>%
  filter(Outcome == 1) %>%
  ggplot(aes(Age, p)) + 
  geom_point() + 
  geom_line(data = LosingSleep, aes(x = Age, y = predict(lm(Outcome ~ Age, data = LosingSleep)))) + 
  ylim(0, 1)

Let’s look at an example

  • 446 teens were asked “On an average school night, do you get at least 7 hours of sleep”
  • Outcome is [1 = “Yes”, 0 = “No”]
  • Is Age related to this outcome?
  • What if I try to fit this as a linear regression model?
Code 
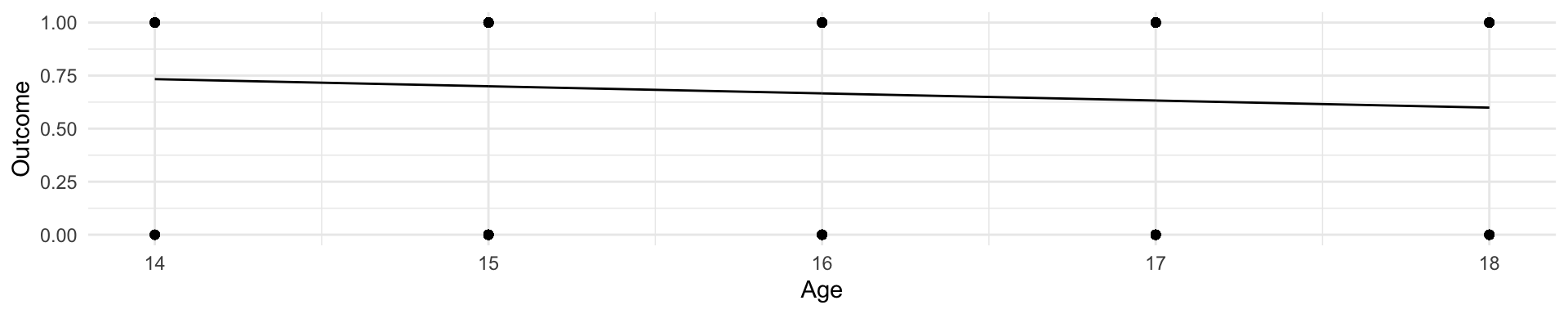
new_data <- data.frame(Age = 0:40)
LosingSleep %>%
  group_by(Age) %>%
  count(Age, Outcome) %>%
  mutate(p = n / sum(n)) %>%
  filter(Outcome == 1) %>%
  ggplot(aes(Age, p)) + 
  geom_point() + 
  geom_line(data = new_data, aes(x = Age, y = predict(lm(Outcome ~ Age, data = LosingSleep), newdata = new_data))) + 
  ylim(-1, 2) + 
  xlim(0, 40) +
  geom_hline(yintercept = c(0, 1), lty = 2)

Let’s look at an example

  • Perhaps it would be sensible to find a function that would not extend beyond 0 and 1?
Code 
LosingSleep %>%
  group_by(Age) %>%
  count(Age, Outcome) %>%
  mutate(p = n / sum(n)) %>%
  filter(Outcome == 1) %>%
  ggplot(aes(Age, p)) + 
  geom_point() + 
  geom_rect(aes(xmin = 0, xmax = 5, ymin = 1, ymax = 1.2), fill = "yellow", color = "black") +
  geom_rect(aes(xmin = 35, xmax = 40, ymin = 0, ymax = -0.2), fill = "yellow", color = "black") +
  geom_line(data = new_data, aes(x = Age, y = predict(lm(Outcome ~ Age, data = LosingSleep), newdata = new_data))) + 
  ylim(-1, 2) + 
  xlim(0, 40) +
  geom_hline(yintercept = c(0, 1), lty = 2)

Let’s look at an example

  • Perhaps it would be sensible to find a function that would not extend beyond 0 and 1?
Code 
LosingSleep %>%
  group_by(Age) %>%
  count(Age, Outcome) %>%
  mutate(p = n / sum(n)) %>%
  filter(Outcome == 1) %>%
  ggplot(aes(Age, p)) + 
  geom_point() + 
  geom_rect(aes(xmin = 0, xmax = 5, ymin = 1, ymax = 1.2), fill = "yellow", color = "black") +
  geom_rect(aes(xmin = 35, xmax = 40, ymin = 0, ymax = -0.2), fill = "yellow", color = "black") +
  geom_line(data = new_data,
            aes(x = Age, y = predict(
              glm(Outcome ~ Age, family = "binomial", data = LosingSleep),
              newdata = new_data,
              type = "response"))) + 
  ylim(-1, 2) + 
  xlim(0, 40) +
  geom_hline(yintercept = c(0, 1), lty = 2)

Let’s look at an example

  • Perhaps it would be sensible to find a function that would not extend beyond 0 and 1?
Code 
LosingSleep %>%
  group_by(Age) %>%
  count(Age, Outcome) %>%
  mutate(p = n / sum(n)) %>%
  filter(Outcome == 1) %>%
  ggplot(aes(Age, p)) + 
  geom_point() + 
  geom_line(data = new_data,
            aes(x = Age, y = predict(
              glm(Outcome ~ Age, family = "binomial", data = LosingSleep),
              newdata = new_data,
              type = "response"))) + 
  xlim(0, 40) +
  geom_hline(yintercept = c(0, 1), lty = 2)
  • this line is fit using logistic regression model

How does this compare to linear regression?

Model Outcome Form
Ordinary linear Regression Numeric \(y \approx \beta_0 + \beta_1 x\)
Number of Doctors example Numeric \(\sqrt{\textrm{Number of doctors}}\approx \beta_0 +\beta_1x\)
Logistic regression Binary \(\log\left(\frac{\pi}{1-\pi}\right) = \beta_0 + \beta_1x\)
  • \(\pi\) is the probability that \(y = 1\) ( \(P(y = 1)\) )

Notation

  • \(\log\left(\frac{\pi}{1-\pi}\right)\): the “log odds”
  • \(\pi\) is the probability that \(y = 1\) - the probability that your outcome is 1.
  • \(\frac{\pi}{1-\pi}\) is a ratio representing the odds that \(y = 1\)
  • \(\log\left(\frac{\pi}{1-\pi}\right)\) is the log odds
  • The transformation from \(\pi\) to \(\log\left(\frac{\pi}{1-\pi}\right)\) is called the logistic or logit transformation

A bit about “odds”

  • The “odds” tell you how likely an event is
  • 👛 if I flip a fair coin, what is the probability that I’d get heads?
    • \(p = 0.5\)
  • What is the probability that I’d get tails?
    • \(1 - p = 0.5\)
  • The odds are 1:1, 0.5:0.5
  • the odds can be written as \(\frac{p}{1-p} =\frac{0.5}{0.5} = 1\)

A bit about “odds”

  • The “odds” tell you how likely an event is
  • ⛱ Let’s say there is a 60% chance of rain today
  • What is the probability that it will rain?
    • \(p = 0.6\)
  • What is the probability that it won’t rain?
    • \(1-p = 0.4\)
  • What are the odds that it will rain?
    • 3 to 2, 3:2, \(\frac{0.6}{0.4} = 1.5\)

Transforming logs

  • How do you “undo” a \(\log\) base \(e\)?
  • Use \(e\)! For example:
    • \(e^{\log(10)} = 10\)
  • \(e^{\log(1283)} = 1283\)
  • \(e^{\log(x)} = x\)

Transforming logs

How would you get the odds from the log(odds)?

  • How do you “undo” a \(\log\) base \(e\)?
  • Use \(e\)! For example:
    • \(e^{\log(10)} = 10\)
    • \(e^{\log(1283)} = 1283\)
    • \(e^{\log(x)} = x\)
  • \(e^{\log(odds)}\) = odds

Transforming odds

  • odds = \(\frac{\pi}{1-\pi}\)
  • Solving for \(\pi\)
    • \(\pi = \frac{\textrm{odds}}{1+\textrm{odds}}\)
  • Plugging in \(e^{\log(odds)}\) = odds
  • \(\pi = \frac{e^{\log(odds)}}{1+e^{\log(odds)}}\)
  • Plugging in \(\log(odds) = \beta_0 + \beta_1x\)
  • \(\pi = \frac{e^{\beta_0 + \beta_1x}}{1+e^{\beta_0 + \beta_1x}}\)

The logistic model

  • ✌️ forms
Form Model
Logit form \(\log\left(\frac{\pi}{1-\pi}\right) = \beta_0 + \beta_1x\)
Probability form \(\Large\pi = \frac{e^{\beta_0 + \beta_1x}}{1+e^{\beta_0 + \beta_1x}}\)

The logistic model

probability odds log(odds)
\(\pi\) \(\frac{\pi}{1-\pi}\) \(\log\left(\frac{\pi}{1-\pi}\right)=l\)

⬅️

log(odds) odds probability
\(l\) \(e^l\) \(\frac{e^l}{1+e^l} = \pi\)

The logistic model

  • ✌️ forms
  • log(odds): \(l = \beta_0 + \beta_1x\)
  • P(Outcome = Yes): \(\Large\pi =\frac{e^{\beta_0 + \beta_1x}}{1+e^{\beta_0 + \beta_1x}}\)

Example

  • We are interested in the probability of getting accepted to medical school given a college student’s GPA
data("MedGPA")
ggplot(MedGPA, aes(Accept, GPA)) + 
  geom_boxplot() + 
  geom_jitter()

Example

What is the equation for the model we are going to fit?

  • We are interested in the probability of getting accepted to medical school given a college student’s GPA

Example

What is the equation for the model we are going to fit?

  • \(\log(odds) = \beta_0 + \beta_1 GPA\)
  • P(Accept) \(= \frac{e^{\beta_0 + \beta_1GPA}}{1+e^{\beta_0 + \beta_1GPA}}\)
  • We are interested in the probability of getting accepted to medical school given a college student’s GPA

Example

  • We are interested in the probability of getting accepted to medical school given a college student’s GPA
glm(Acceptance ~ GPA, data = MedGPA,
    family = "binomial") 

Call:  glm(formula = Acceptance ~ GPA, family = "binomial", data = MedGPA)

Coefficients:
(Intercept)          GPA  
    -19.207        5.454  

Degrees of Freedom: 54 Total (i.e. Null);  53 Residual
Null Deviance:      75.79 
Residual Deviance: 56.84    AIC: 60.84

Example

  • We are interested in the probability of getting accepted to medical school given a college student’s GPA
glm(Acceptance ~ GPA, data = MedGPA,
    family = "binomial") %>%
  fitted() 
         1          2          3          4          5          6          7 
0.63124876 0.85036851 0.16944765 0.71491359 0.31617156 0.74706022 0.88186412 
         8          9         10         11         12         13         14 
0.27099332 0.73661581 0.88186412 0.92030775 0.45723876 0.79506038 0.61846455 
        15         16         17         18         19         20         21 
0.23009846 0.52528952 0.66845438 0.52528952 0.18535740 0.88186412 0.73661581 
        22         23         24         25         26         27         28 
0.79506038 0.89276358 0.87606259 0.70366831 0.55238896 0.39074729 0.57918073 
        29         30         31         32         33         34         35 
0.34021444 0.83595184 0.63124876 0.08681729 0.88186412 0.72589836 0.17726253 
        36         37         38         39         40         41         42 
0.86372477 0.52528952 0.34021444 0.87001815 0.11101432 0.30449919 0.31617156 
        43         44         45         46         47         48         49 
0.63124876 0.90745180 0.30449919 0.29307306 0.92030775 0.06749390 0.22057873 
        50         51         52         53         54         55 
0.69217046 0.01247874 0.55238896 0.44373791 0.01917403 0.39074729

Dr. Lucy D’Agostino McGowan